Impact Responses of Prismatic Lithium-Ion Battery Based on the Membrane Factor Method
-
摘要:
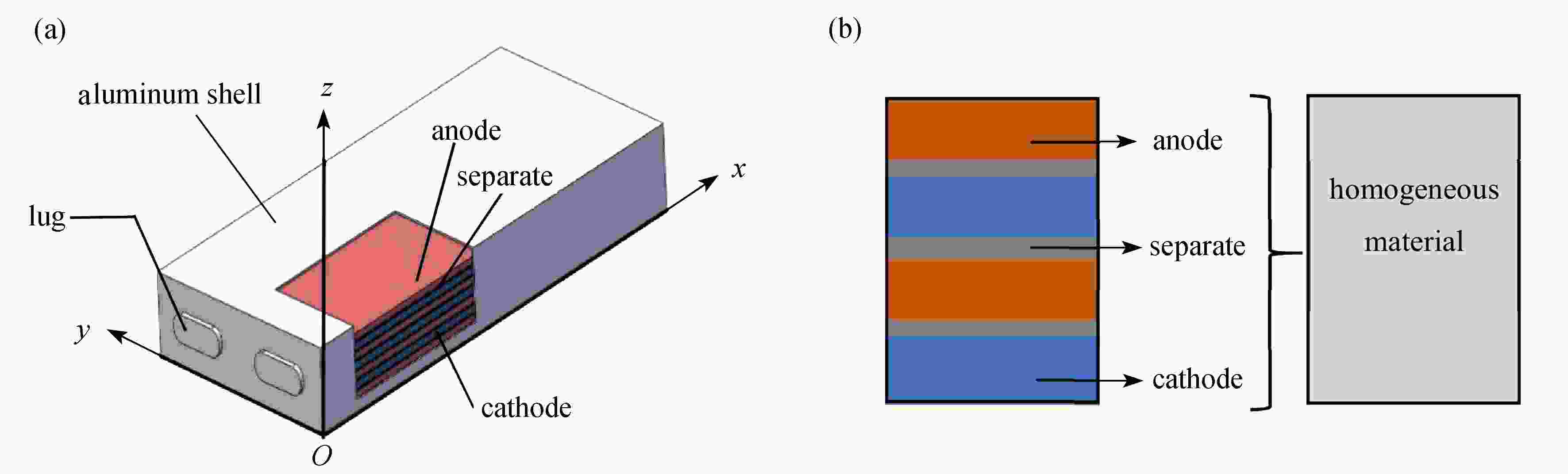
针对锂离子电池在冲击载荷下的大变形短路问题，首先建立了方形电池的简化模型，基于膜力因子法推导出电池在冲击载荷下的速度和位移运动方程。考虑到外壳厚度和芯材密度的因素，具体研究了方形锂离子电池的冲击动力响应特性。研究表明，通过引入膜力因子法改进的运动方程能够反映电池在冲击载荷下的动态响应机制，预测高速冲击下方形电池的大挠度变形。锂离子电池下部外壳的变形随电池外壳厚度的增加而减小，而电池芯材密实区域随外壳厚度的增加而增加。电池下部外壳的变形和密实区域均随电池内芯密度增加而增大。该文所提出的冲击模型可为方形锂离子电池的动力学性能多功能一体化设计提供理论参考。
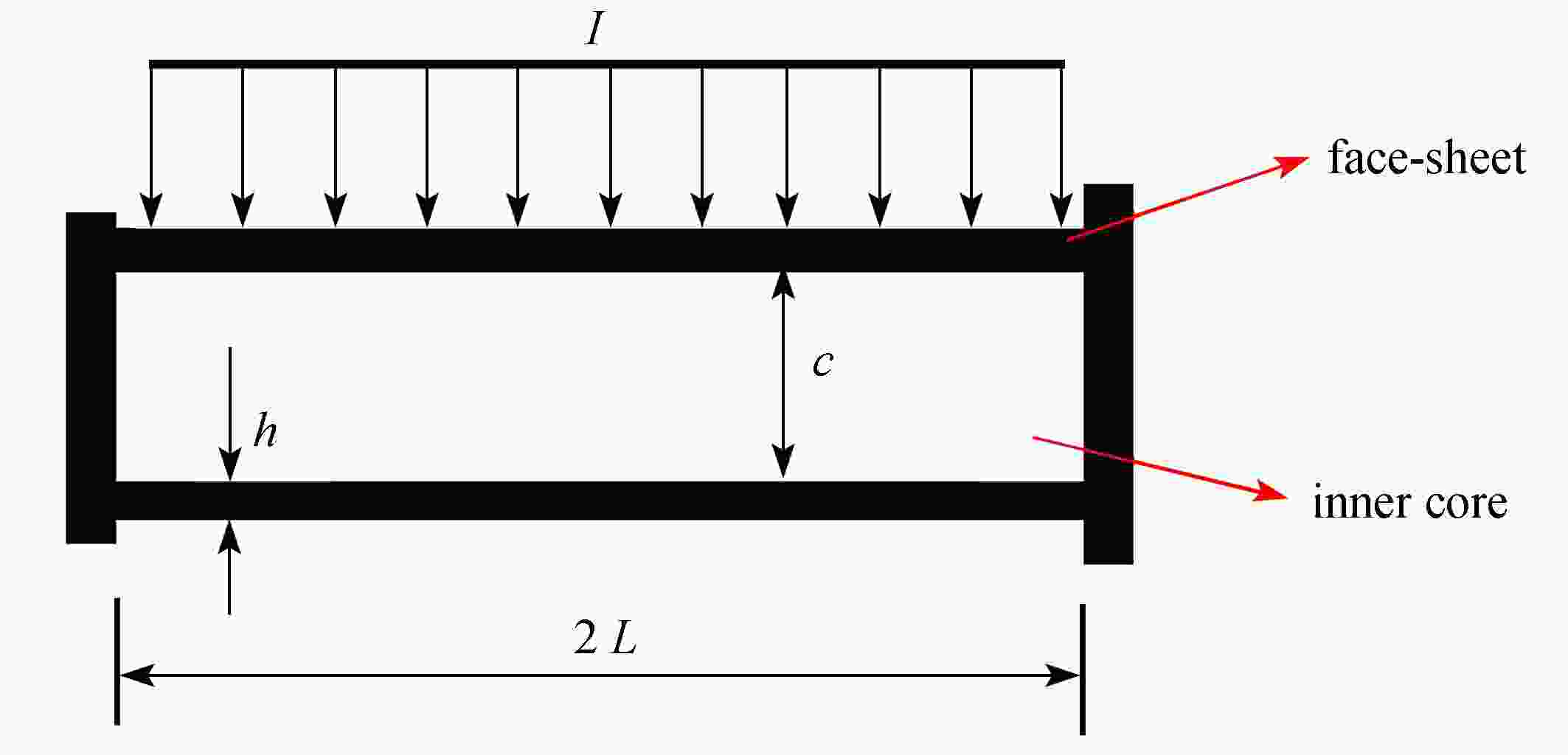
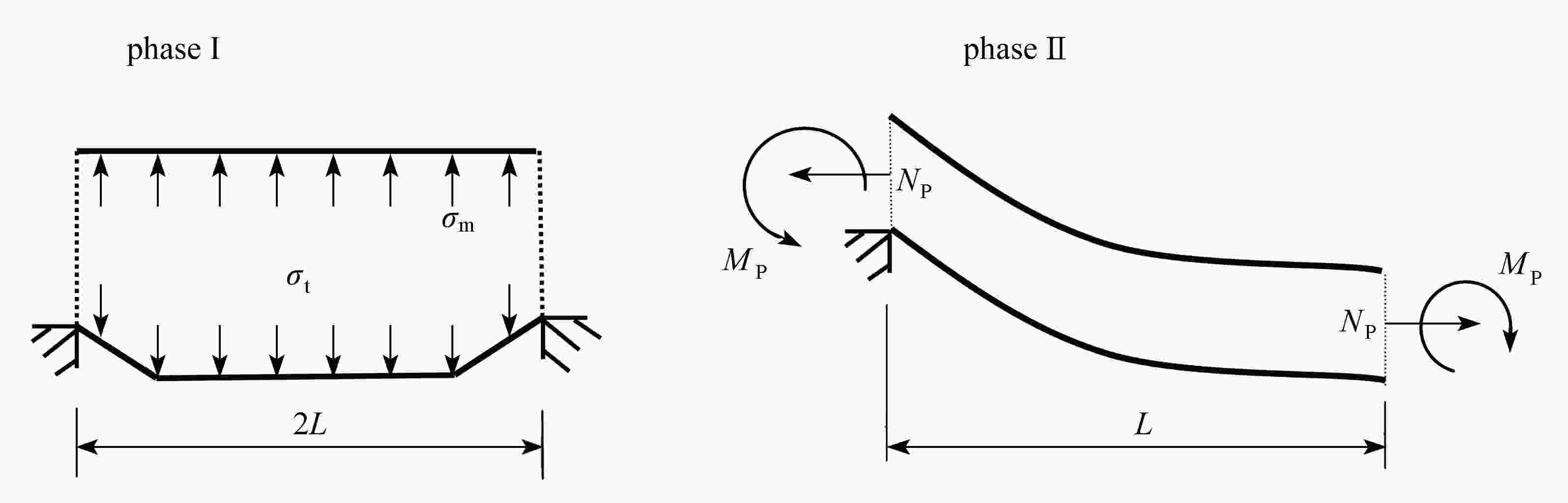
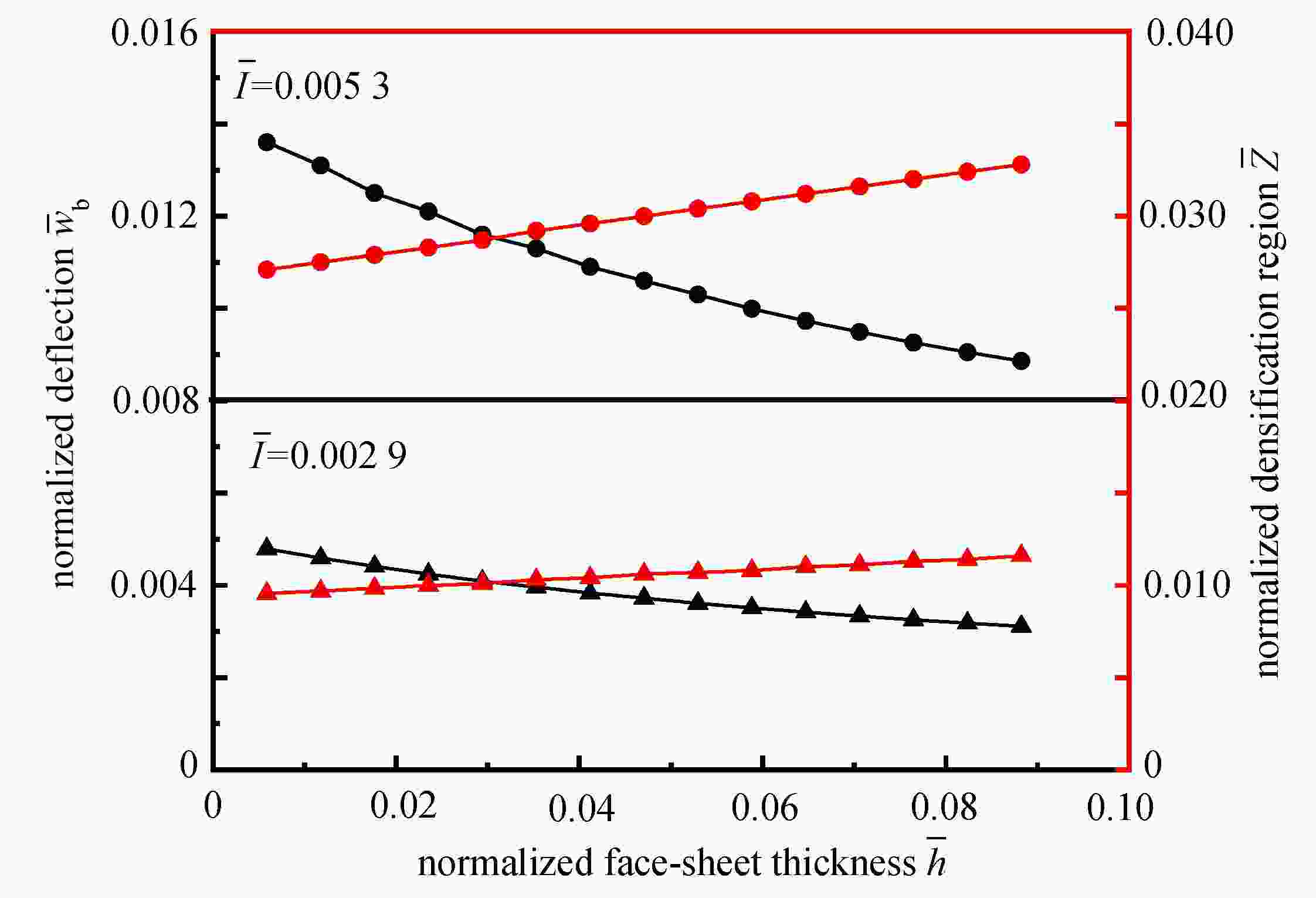
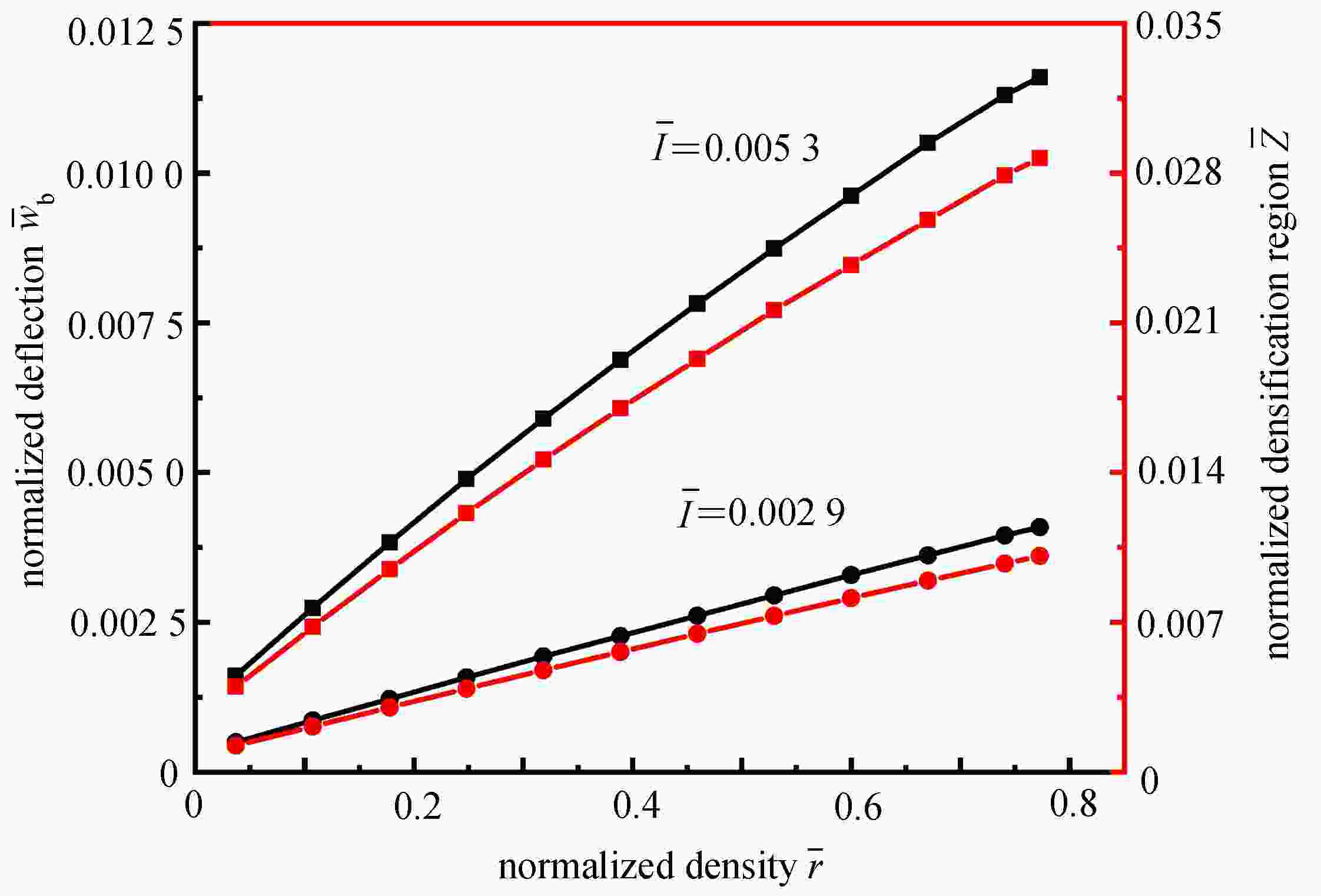
Abstract:Aimed at the internal short circuit problem due to large deformation of the prismatic lithium-ion battery cell under impact loadings, a simplified battery model was first established. Then the motion equations of velocity and displacement based on the membrane factor method were proposed. With the effects of the face-sheet thickness and the densification region on the normalized final deflection, impact response characteristics of prismatic battery cells were investigated in detail. The results show that, the improved motion equations involving the membrane factor can reflect the dynamic response mechanisms of the prismatic battery cell under impact loadings, and the large deflection under high-speed impact can be predicted. With the increase of the face-sheet thickness, the deflection of the battery cell’s lower part decreases obviously. However, the densification region expands with the face-sheet thickness. The deflection and the densification region of the cell’s lower part both increase with the inner core density of the battery. This proposed impact model provides a theoretical guidance for the multi-functional integrated dynamic design of prismatic battery cells.
-
图 1 方形锂离子电池结构及内芯简化示意图：(a) 方形电池结构；(b) 内芯的各向同性均质模型
Figure 1. Schematic diagram of the prismatic lithium-ion battery and the corresponding simplified structure of the inner core: (a) the prismatic cell structure; (b) the isotropic homogeneous model for the inner core
图 2 锂离子电池简化结构冲击响应模型
Figure 2. The impact response model for the simplified structure of a battery
图 4 锂离子电池运动的两种变形状态：(a) 内芯不完全致密化；(b) 内芯完全致密化
Figure 4. Two deformation states of the lithium-ion battery: (a) the incomplete core densification; (b) the complete core densification
图 6 方形锂离子电池的冲击响应时间历程分析：(a) 上下部外壳的无量纲速度；(b) 下部外壳的无量纲挠度
Figure 6. Time histories of impact responses of prismatic lithium-ion battery: (a) normalized velocities of the upper and lower face sheets; (b) normalized deflections of the lower face sheet
图 7 面板厚度对最终无量纲挠度和致密化区域的影响
Figure 7. Effects of the face sheet thickness on the normalized final deflection and the densification region
图 8 芯材相对密度对最终无量纲挠度的影响
Figure 8. Effects of the normalized density of the lithium-ion battery inner core on the normalized final deflection
图 9 不同冲量下方形锂离子电池下部外壳挠度的时间历程
Figure 9. Time histories of normalized deflections of the lower face sheet for the prismatic lithium-ion battery under different impulses
表 1 模型无量纲参数
Table 1. Model dimensionless parameters
$\bar h$ $\bar c$ εd $\bar \sigma $ $\bar \rho $ $\bar I$ 0.0294 0.2429 0.157 0.461 0.7726 6.339e−4 
下载: 导出CSV
表 2 方形电池材料参数
Table 2. Material parameters of the lithium-ion battery
Poisson’s ratio μ modulus of elasticity
E/MPayield strength σf /MPa density
ρc/(kg/m3)battery core material 0.01 368 27 2 086 battery housing 0.33 69 000 75.8 2 700
下载: 导出CSV
-
[1] BAI J L, WANG Z R, GAO T F, et al. Effect of mechanical extrusion force on thermal runaway of lithium-ion batteries caused by flat heating[J]. Journal of Power Sources, 2021, 507: 230305. doi: 10.1016/j.jpowsour.2021.230305 [2] 赖铱麟, 杨凯, 刘皓, 等. 锂离子电池安全预警方法综述[J]. 储能科学与技术, 2020, 9(6): 1926-1932 doi: 10.19799/j.cnki.2095-4239.2020.0158LAI Yilin, YANG Kai, LIU Hao, et al. Lithium-ion battery safety warning methods review[J]. Energy Storage Science and Technology, 2020, 9(6): 1926-1932.(in Chinese) doi: 10.19799/j.cnki.2095-4239.2020.0158 [3] 朱伟杰, 董缇, 张树宏. 储能系统锂离子电池国内外安全标准对比分析[J]. 储能科学与技术, 2020, 9(5): 279-286 doi: 10.19799/j.cnki.2095-4239.2019.0199ZHU Weijie, DONG Ti, ZHANG Shuhong. Comparative analysis of domestic and foreign safety standards for lithium-ion batteries for energy storage system[J]. Energy Storage Science and Technology, 2020, 9(5): 279-286.(in Chinese) doi: 10.19799/j.cnki.2095-4239.2019.0199 [4] YIN H F, MA S, LI H G, et al. Modeling strategy for progressive failure prediction in lithium-ion batteries under mechanical abuse[J]. eTransportation, 2020, 7(2): 100098. [5] SHEIKH M, ELMARAKBI A, REHMAN S. A combined experimental and simulation approach for short circuit prediction of 18650 lithium-ion battery under mechanical abuse conditions[J]. Journal of Energy Storage, 2020, 32: 101833. doi: 10.1016/j.est.2020.101833 [6] 兰凤崇, 郑文杰, 李志杰, 等. 车用动力电池的挤压载荷变形响应及内部短路失效分析[J]. 华南理工大学学报(自然科学版), 2018, 46(6): 65-72LAN Fengchong, ZHENG Wenjie, LI Zhijie, et al. Compression load-deformation response and internal short circuit failure analysis of vehicle powered batteries[J]. Journal of South China University of Technology (Natural Science Edition) , 2018, 46(6): 65-72.(in Chinese) [7] XI S J, ZHAO Q C, CHANG L J, et al. The dynamic failure mechanism of a lithium-ion battery at different impact velocity[J]. Engineering Failure Analysis, 2020, 116: 104747. doi: 10.1016/j.engfailanal.2020.104747 [8] MO F H, TIAN Y, ZHAO S Q, et al. Working temperature effects on mechanical integrity of cylindrical lithium-ion batteries[J]. Engineering Failure Analysis, 2022, 137: 106399. doi: 10.1016/j.engfailanal.2022.106399 [9] XU J, LIU B H, HU D Y. State of charge dependent mechanical integrity behavior of 18650 lithium-ion batteries[J]. Scientific Reports, 2016, 6: 21829. doi: 10.1038/srep21829 [10] CHEN Y Y, SANTHANAGOPALAN S, BABU V, et al. Dynamic mechanical behavior of lithium-ion pouch cells subjected to high-velocity impact[J]. Composite Structures, 2019, 218: 50-59. doi: 10.1016/j.compstruct.2019.03.046 [11] CHUNG S H, TANCOGNE-DEJEAN T, ZHU J, et al. Failure in lithium-ion batteries under transverse indentation loading[J]. Journal of Power Sources, 2018, 389: 148-159. doi: 10.1016/j.jpowsour.2018.04.003 [12] 李梦, 柳小伟, 张舒, 等. 轴向压缩下圆柱形动力锂离子电池的性能[J]. 高压物理学报, 2021, 35(3): 179-186 doi: 10.11858/gywlxb.20200647LI Meng, LIU Xiaowei, ZHANG Shu, et al. Performance of cylindrical power lithium-ion battery under axial compression[J]. Chinese Journal of High Pressure Physics, 2021, 35(3): 179-186.(in Chinese) doi: 10.11858/gywlxb.20200647 [13] 董思捷, 张新春, 汪玉林, 等. 不同挤压载荷下圆柱形锂离子电池的失效机理试验研究[J]. 中国机械工程, 2022, 33(8): 915-920, 951 doi: 10.3969/j.issn.1004-132X.2022.08.005DONG Sijie, ZHANG Xinchun, WANG Yulin, et al. Experimental study on the failure mechanism of cylindrical lithium-ion battery under different compression loadings[J]. China Mechanical Engineering, 2022, 33(8): 915-920, 951.(in Chinese) doi: 10.3969/j.issn.1004-132X.2022.08.005 [14] YU T X, CHEN F L. The large deflection dynamic plastic response of rectangular plates[J]. International Journal of Impact Engineering, 1992, 12(4): 605-616. doi: 10.1016/0734-743X(92)90261-Q [15] QIN Q H, WANG T J, ZHAO S Z. Large deflections of metallic sandwich and monolithic beams under locally impulsive loading[J]. International Journal of Mechanical Sciences, 2009, 51(11): 752-773. [16] QIN Q H, WANG T J. A theoretical analysis of the dynamic response of metallic sandwich beam under impulsive loading[J]. European Journal of Mechanics A: Solids, 2009, 28(5): 1014-1025. doi: 10.1016/j.euromechsol.2009.04.002 [17] JIANG W Z, LIU Y, WANG B. Dynamic responses of metal sandwich beams under high velocity impact considering time inhomogeneity of core deformation[J]. International Journal of Impact Engineering, 2017, 110: 311-323. doi: 10.1016/j.ijimpeng.2017.05.010 [18] JIANG W Z, LIU Y, WANG B. The plastic behavior of sandwich beams with core gradation[J]. International Journal of Mechanical Sciences, 2017, 130: 19-30. doi: 10.1016/j.ijmecsci.2017.05.020 [19] 杜志鹏, 张磊, 谌勇, 等. 泡沫覆盖层对水下爆炸气泡射流防护机理缩比试验研究[J]. 应用数学和力学, 2022, 43(5): 569-576DU Zhipeng, ZHANG Lei, CHEN Yong, et al. Foam layer protective mechanism of shrinkage ratio of underwater explosion bubble jet experimental study[J]. Applied Mathematics and Mechanics, 2022, 43(5): 569-576.(in Chinese) [20] 柳占立, 初东阳, 王涛, 等. 爆炸和冲击载荷下金属材料及结构的动态失效仿真[J]. 应用数学和力学, 2021, 42(1): 1-14 doi: 10.1007/s10483-021-2692-5LIU Zhanli, CHU Dongyang, WANG Tao, et al. The explosion and the structure of the metal materials under impact load and dynamic failure simulation[J]. Applied Mathematics and Mechanics, 2021, 42(1): 1-14.(in Chinese) doi: 10.1007/s10483-021-2692-5 [21] 余同希, 朱凌, 许骏. 结构冲击动力学进展(2010‒2020年)[J]. 爆炸与冲击, 2021, 41(12): 121401YU Tongxi, ZHU Ling, XU Jun. Progress in structural impact dynamics (2010‒2020)[J]. Explosion and Shock Waves, 2021, 41(12): 121401.(in Chinese) [22] TILBROOK M T, DESHPANDE V S, FLECK N A. The impulsive response of sandwich beams: analytical and numerical investigation of regimes of behaviour[J]. Journal of the Mechanics and Physics of Solids, 2006, 54(11): 2242-2280. doi: 10.1016/j.jmps.2006.07.001 -
计量
- 文章访问数: 717
- HTML全文浏览量: 273
- PDF下载量: 68
- 被引次数: 0
渝公网安备50010802005915号