内爆载荷作用下泄压容器准静态压力特性

解江; 潘汉源; 李漩; 王立轩; 蒋逸伦; 冯振宇

doi:10.21656/1000-0887.430359

内爆载荷作用下泄压容器准静态压力特性

doi: 10.21656/1000-0887.430359

解江^{1, 2, ,},
潘汉源^{2, 3},
李漩^{2, 3},
王立轩^{2, 3},
蒋逸伦^{2, 3},
冯振宇^{1, 2}

1.
中国民航大学科技创新研究院，天津 300300
2.
民航航空器适航审定技术重点实验室，天津 300300
3.
中国民航大学安全科学与工程学院，天津 300300

详细信息

通讯作者:
解江(1982—)，男，副研究员，博士，硕士生导师(通讯作者. E-mail: xiejiang5@126.com)

中图分类号: O383
计量
- 文章访问数: 314
- HTML全文浏览量: 150
- PDF下载量: 44
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-08
- 修回日期: 2023-07-10
- 刊出日期: 2023-10-31

Quasi-Static Pressure Characteristics of Explosion Venting Vessel Under Confined Explosion

XIE Jiang^{1, 2
, ,},
PAN Hanyuan^{2, 3},
LI Xuan^{2, 3},
WANG Lixuan^{2, 3},
JIANG Yilun^{2, 3},
FENG Zhenyu^{1, 2}

1.
Science and Technology Innovation Research Institute, Civil Aviation University of China, Tianjin 300300, P.R. China
2.
Key Laboratory of Civil Aviation Aircraft Airworthiness Certification Technology, Tianjin 300300, P.R. China
3.
College of Safety Science and Engineering, Civil Aviation University of China, Tianjin 300300, P.R. China

摘要

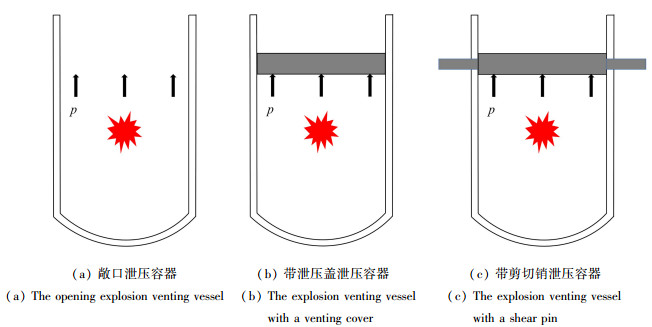
摘要: 为了研究泄压容器内部准静态压力特性，采用AUTODYN软件提出并建立了3种柱形泄压容器的数值模型，分别包括一端开口的敞口泄压容器、在开口处设有可冲出端盖的带泄压盖容器、将泄压盖与容器通过剪切销连接的带剪切销泄压容器. 以Bernoulli方程为基础建立了理论简化模型，模拟了敞口泄压容器内部的准静态压力；以能量守恒方程为基础建立理论简化模型，模拟了不同起爆药量下带泄压盖容器的准静态压力；最后，探讨了剪切销在剪断和未剪断时对带剪切销泄压容器内部压力的影响. 该文建立了文献中的数值模型，准静态压力计算结果与文献中的实验结果吻合情况良好，验证了计算方法的可靠性. 结果表明：敞口泄压容器内部压力衰减迅速，准静态阶段持续时间较短，以Bernoulli方程为基础的理论简化模型能够较好地预测泄压容器内部压力衰减至大气压力的时间；带泄压盖容器内冲击波沿轴向做往复式传播，以能量守恒方程为基础的理论模型能够较好地预测在泄压过程中的准静态压力；剪切销未剪断时，容器内部准静态压力呈现明显的平台效应；对比无剪切销的工况，18 mm直径的剪切销剪断后，容器内部压力变化趋势基本一致，泄压盖的飞出时间提前了0.25 ms. 研究结果可为泄压容器的结构设计提供理论基础和参考.
- 泄压容器 /
- 泄压盖 /
- 内爆炸 /
- 准静态压力
Abstract: To study the quasi-static pressure characteristics inside the explosion venting vessels, 3 numerical models for cylindrical explosion venting vessels were established with the AUTODYN software, including a one-end-opening explosion venting vessel, an explosion venting vessel with an ejectable venting cover, and an explosion venting vessel with a shear pinned venting cover. Based on the Bernoulli equation, a theoretical simplified model was established to simulate the quasi-static pressure inside the opening explosion venting vessel. A theoretical simplified model based on the energy conservation equation was established to simulate the quasi-static pressure in the vessel with a venting cover under different charge weights. In the end, the effects of the shear pin on the pressure of the explosion venting vessel were discussed in the cases of cutoff or non-cutoff. The numerical models in previous literatures were established. The theoretical quasi-static pressure results are in good agreement with the experimental results in the literatures, which verifies the reliability of the proposed theoretical calculation method. The results show that, the internal pressure of the open explosion venting vessel decays rapidly, and the quasi-static stage lasts for a short time. The theoretical simplified model based on the Bernoulli equation can better predict the time when the internal pressure in the explosion venting vessel decays to the atmospheric pressure. The shock wave in the vessel with a venting cover propagates reciprocally along the axial direction. The theoretical model based on the energy conservation equation can better predict the quasi-static pressure during the pressure decaying process. In the case of the non-cutoff shear pin, the quasi-static pressure inside the vessel exhibits an obvious platform effect. Compared with the case without a shear pin, the internal pressure in the vessel with a shear pin will decay basically in the same way after the shear pin with a diameter of 18 mm is cut off, and the venting cover will reach the opening in advance by 0.25 ms. This work mainly provides a theoretical basis and applicable reference for the structural design of explosion venting vessels.
- explosion venting vessel /
- venting cover /
- confined explosion /
- quasi-static pressure

HTML全文

图 1 3种泄压容器示意图

Figure 1. Schematic diagram of 3 explosion venting vessels

下载: 全尺寸图片幻灯片

图 2 密闭爆炸容器数值模型

Figure 2. The numerical model for the closed explosion vessel

下载: 全尺寸图片幻灯片

图 3 数值模拟密闭容器内部冲击波超压时程曲线

Figure 3. The numerical simulation of shock wave pressure-time curves inside the closed vessel

下载: 全尺寸图片幻灯片

图 4 3种泄压容器几何模型(单位: mm)

Figure 4. Geometric models for 3 explosion venting vessels(unit: mm)

下载: 全尺寸图片幻灯片

图 5 内部压力理论计算值与数值模拟测量值对比

Figure 5. Comparison between theoretical calculation values and numerical simulation values of the internal pressure

下载: 全尺寸图片幻灯片

图 6 泄压盖速度-时间曲线

注为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.

Figure 6. Venting cover velocity-time curves

下载: 全尺寸图片幻灯片

图 7 带泄压盖容器内部理论计算超压平均值与数值模拟测量值对比

Figure 7. Comparison between the average theoretical overpressure values and the numerical simulation values in the explosion venting vessel with a venting cover

下载: 全尺寸图片幻灯片

图 8 剪切销未断裂时容器内准静态超压理论与数值计算对比

Figure 8. Comparison between theoretical quasi-static overpressure values and numerical values in the vessel with the shear pin unbroken

下载: 全尺寸图片幻灯片

图 9 不同剪切销直径下泄压容器内部超压-时间曲线

Figure 9. Pressure-time curves of the explosion venting vessel under different shear pin diameters

下载: 全尺寸图片幻灯片

表 1 15-5PH材料参数^[19]

Table 1. Material parameters of 15-5PH^[19]

parameter	value	parameter	value
density ρ_15-5PH/(kg/m³)	7.78×10³	E/GPa	196.51
Poisson’s ratio μ	0.27	yield strength σ_y	1.077
B	0.499	n	0.568
failure strain ε₀	0.22

下载: 导出CSV

表 2 JWL状态方程参数^[23]

Table 2. EOS parameters of JWL^[23]

parameter	value	parameter	value
A/GPa	374	B/GPa	3.74
R₁	4.15	R₂	1.4
ω	0.35	E₀/GPa	7
V	1	density ρ_TNT/(g/cm³)	1.63
detonation velocity D/(m/s)	6 930	Chapman-Jouguet pressure P_CJ/GPa	21

下载: 导出CSV

表 3 本文准静态压力数值模拟值与文献[24]中的试验值对比情况

Table 3. Comparison of the numerical simulation quasi-static pressure in this paper and the experimental quasi-static pressure in ref. [24]

TNT charge mass W_TNT/g	quasi-static pressure in the closed explosion vessel
TNT charge mass W_TNT/g	numerical simulation ρ_n/MPa	experimental result^[24] ρ_e/MPa	error δ/%
5	20.91	22.46	6.9
10	42.03	45.10	6.81
15	62.61	68.25	8.26

下载: 导出CSV

表 4 本文准静态压力理论预测值与文献[24]中的试验值对比情况

Table 4. Comparison of the theoretical quasi-static pressure in this paper and the experimental quasi-static pressure in ref. [24]

TNT charge mass W_TNT/g	quasi-static pressure in the closed explosion vessel
TNT charge mass W_TNT/g	theoretical prediction p_t/MPa	experimental result^[24] p_e/MPa	error δ/%
5	24.06	22.46	7.12
10	48.12	45.10	6.70
15	72.18	68.25	5.76

下载: 导出CSV

表 5 对比不同剪切销直径对准静态压力与泄压盖出口速度的影响

Table 5. Comparison of the effects of different shear pin diameters on the quasi-static pressure and the cover velocity

shear pin diameter d/mm	quasi-static pressure when the cover reached the vessel opening p_c/MPa	velocity of the cover reaching the vessel opening v_c/(m/s)	time of the cover reaching the vessel opening t_c/ms
no shear pin	10.3	131.72	2
10	9.09	125.9	2.1
18	8.67	120.92	2.25

下载: 导出CSV

参考文献(32)

[1]	SIWEK R. Explosion venting technology[J]. Journal of Loss Prevention in the Process Industries, 1996, 9(1): 81-90. doi: 10.1016/0950-4230(95)00058-5
[2]	赵天辉, 高康华, 王明洋, 等. 方形容器爆燃泄放过程中的压力特性实验研究[J]. 兵工学报, 2017, 38(4): 722-727. doi: 10.3969/j.issn.1000-1093.2017.04.013 ZHAO Tianhui, GAO Kanghua, WANG Mingyang, et al. Experimental study of pressure characteristics during deflagration venting in a square vessel[J]. Acta Armamentarii, 2017, 38(4): 722-727. (in Chinese) doi: 10.3969/j.issn.1000-1093.2017.04.013
[3]	张玉磊, 苏健军, 李芝绒, 等. TNT内爆炸准静态压力特性[J]. 爆炸与冲击, 2018, 38(6): 1429-1434. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201806029.htm ZHANG Yulei, SU Jianjun, LI Zhirong, et al. Quasi-static pressure characteristic of TNT's internal explosion[J]. Explosion and Shock Waves, 2018, 38(6): 1429-1434. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201806029.htm
[4]	徐维铮, 吴卫国. 泄压口大小对约束空间爆炸准静态超压载荷的影响规律[J]. 高压物理学报, 2017, 31(5): 619-628. https://www.cnki.com.cn/Article/CJFDTOTAL-GYWL201705016.htm XU Weizheng, WU Weiguo. Effects of size of venting holes on the characteristics of quasi-static overpressure in confined space[J]. Chinese Journal of High Pressure Physics, 2017, 31(5): 619-628. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYWL201705016.htm
[5]	BAKER W E, OLDHAM G A. Estimates of blowdown of quasi-static pressures in vented chambers: EM-CR-76029[R]. Southwest Research Institute, 1975.
[6]	张玉磊, 陈华, 韩璐, 等. 泄压口面积对温压炸药内爆炸准静态压力的影响[J]. 火炸药学报, 2020, 43(5): 521-525. doi: 10.14077/j.issn.1007-7812.201909024 ZHANG Yulei, CHEN Hua, HAN Lu, et al. Effect of venting area on quasi-static pressure of internal explosion for thermobaric explosive[J]. Chinese Journal of Explosives and Propellants, 2020, 43(5): 521-525. (in Chinese) doi: 10.14077/j.issn.1007-7812.201909024
[7]	徐维铮, 吴卫国. 装药质量对约束空间内爆炸准静态超压载荷的影响规律研究[J]. 应用力学学报, 2018, 35(1): 42-46. https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201801007.htm XU Weizheng, WU Weiguo. Influence of mass of explosives on the characteristics of quasi-static overpressure in confined space[J]. Chinese Journal of Applied Mechanics, 2018, 35(1): 42-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYLX201801007.htm
[8]	高轩能, 王书鹏, 江媛. 爆炸荷载下大空间结构的冲击波压力场分布及泄爆措施研究[J]. 工程力学, 2010, 27(4): 226-233. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201004039.htm GAO Xuanneng, WANG Shupeng, JIANG Yuan. Shock wave pressure distribution on large-space structure and explosion venting under blast loading[J]. Engineering Mechanics, 2010, 27(4): 226-233. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201004039.htm
[9]	汪维, 刘瑞朝, 吴飚, 等. 建筑物内爆泄压口冲击波参数工程算法研究[J]. 振动与冲击, 2015, 34(9): 48-54. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201509011.htm WANG Wei, LIU Ruichao, WU Biao, et al. Engineering arithmetic for internal blast waves parameters in venting area of building structures[J]. Journal of Vibration and Shock, 2015, 34(9): 48-54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201509011.htm
[10]	宋浦, 冯海云, 胡宏伟, 等. 爆炸装药在有限空间内爆炸做功能力的一种新型评估方法[J]. 防护工程, 2014, 36(2): 26-28. https://www.cnki.com.cn/Article/CJFDTOTAL-FHGC201402007.htm SONG Pu, FENG Haiyun, HU Hongwei, et al. A new evaluation method for charge work capacity exploding in finite space[J]. Projective Engineering, 2014, 36(2): 26-28. https://www.cnki.com.cn/Article/CJFDTOTAL-FHGC201402007.htm
[11]	李根, 卢芳云, 李翔宇. 测量炸药爆炸威力的实验方法研究[J]. 中国测试, 2020, 46(9): 40-46. https://www.cnki.com.cn/Article/CJFDTOTAL-SYCS202009007.htm LI Gen, LU Fangyun, LI Xiangyu. Research on experimental method for assessing explosive power[J]. China Measurement & Test, 2020, 46(9): 40-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SYCS202009007.htm
[12]	胡宏伟, 冯海云, 肖川, 等. 基于顶盖举起试验的炸药内爆炸性能评估[J]. 火炸药学报, 2016, 39(3): 53-57. https://www.cnki.com.cn/Article/CJFDTOTAL-BGXB201603011.htm HU Hongwei, FENG Haiyun, XIAO Chuan, et al. Evaluation of the internal blast performance of explosives based on roof lift test[J]. Chinese Journal of Explosives & Propellants, 2016, 39(3): 53-57. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BGXB201603011.htm
[13]	FELDGUN V R, KARINSKI Y S, YANKELEVSKY D Z. A simplified model with lumped parameters for explosion venting simulation[J]. International Journal of Impact Engineering, 2011, 38(12): 964-975.
[14]	FELDGUN V R, KARINSKI Y S, YANKELEVSKY D Z. Simplified models of shock waves interaction with rigid and flexible obstacles[C]// 30 th International Symposium on Shock Waves 1 . Switzerland, 2017: 691-696.
[15]	FELDGUN V R, KARINSKI Y S, EDRI I, et al. On blast pressure analysis due to a partially confined explosion Ⅱ: numerical studies[J]. International Journal of Protective Structures, 2012, 3(1): 61-79.
[16]	MOLKOV V V, GRIGORASH A V, EBER R M, et al. Vented gaseous deflagrations: modelling of translating inertial vent covers[J]. Journal of Loss Prevention in the Process Industries, 2003, 16(5): 395-402.
[17]	YANKELEVSKY D Z, FELDGUN V R, KARINSKI Y S, et al. Prediction of quasi-static pressure in confined and partially confined explosions and its application to blast response simulation of flexible structures[J]. International Journal of Impact Engineering, 2016, 90: 46-60.
[18]	柳占立, 初东阳, 王涛, 等. 爆炸和冲击载荷下金属材料及结构的动态失效仿真[J]. 应用数学和力学, 2021, 42(1): 1-14. doi: 10.21656/1000-0887.410262 LIU Zhanli, CHU Dongyang, WANG Tao, et al. Dynamic failure simulation of metal materials and structures under blast and impact loading[J]. Applied Mathematics and Mechanics, 2021, 42(1): 1-14. (in Chinese) doi: 10.21656/1000-0887.410262
[19]	戴志成. 飞机断离销剪切强度有限元与实验研究[D]. 硕士学位论文. 沈阳: 沈阳理工大学, 2017. DAI Zhicheng. Finite element and experimental study on shear strength of aircraft fuse pin[D]. Master Thesis. Shenyang: Shenyang Ligong University, 2017. (in Chinese)
[20]	李臻, 刘彦, 黄风雷, 等. 接触爆炸和近距离爆炸比冲量数值仿真研究[J]. 北京理工大学学报, 2020, 40(2): 143-149. https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG202002005.htm LI Zhen, LIU Yan, HUANG Fenglei, et al. Investigation of specific impulse under contact explosion and close-in explosion conditions using numerical method[J]. Transactions of Beijing Institute of Technology, 2020, 40(2): 143-149. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJLG202002005.htm
[21]	王辉. 炸药爆炸产物JWL状态方程参数数值计算[D]. 硕士学位论文. 西安: 西安工业大学, 2011. WANG Hui. Numerical calculation of parameters of JWL equation of state for explosive explosion products[D]. Master Thesis. Xi'an: Xi'an Industrial University, 2011. (in Chinese)
[22]	冯振宇, 姜超, 高斌元, 等. 芳纶纤维平纹织布在爆炸载荷下的动态响应与失效行为的数值分析[J]. 应用数学和力学, 2021, 42(11): 1113-1125. doi: 10.21656/1000-0887.420025 FENG Zhenyu, JIANG Chao, GAO Binyuan, et al. Numerical study on dynamic responses and failure behaviours of aramid fabrics subject to blast loads[J]. Applied Mathematics and Mechanics, 2021, 42(11): 1113-1125. (in Chinese) doi: 10.21656/1000-0887.420025
[23]	解江, 高斌元, 甄婷婷, 等. 爆炸载荷下机织物的动态响应与失效行为[J]. 复合材料学报, 2022, 39(10): 4949-4960. https://www.cnki.com.cn/Article/CJFDTOTAL-FUHE202210051.htm XIE Jiang, GAO Binyuan, ZHEN Tingting, et al. Dynamic response and failure behaviors of woven fabrics under blast load[J]. Acta Materiae Compositae Sinica, 2022, 39(10): 4949-4960. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FUHE202210051.htm
[24]	王鑫, 张连生, 张明明, 等. 密闭空间TNT内爆炸准静态压力研究[J]. 兵器装备工程学报, 2020, 41(5): 188-192. https://www.cnki.com.cn/Article/CJFDTOTAL-CUXI202005036.htm WANG Xin, ZHANG Liansheng, ZHANG Mingming, et al. Study on quasi-static pressure of TNT internal explosion in confined spaces[J]. Journal of Ordnance Equipment Engineering, 2020, 41(5): 188-192. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CUXI202005036.htm
[25]	徐维铮, 吴卫国. JWL状态方程及其等效多方状态方程在内爆炸计算中的应用分析[J]. 中国舰船研究, 2019, 14(3): 83-91. https://www.cnki.com.cn/Article/CJFDTOTAL-JCZG201903011.htm XU Weizheng, WU Weiguo. Application analysis of JWL EOS and the equivalent polytropic EOS in internal explosion calculation[J]. Chinese Journal of Ship Research, 2019, 14(3): 83-91. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JCZG201903011.htm
[26]	孔祥韶, 王子棠, 况正, 等. 密闭空间内爆炸载荷抑制效应实验研究[J]. 爆炸与冲击, 2021, 41(6): 24-37. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ202106003.htm KONG Xiangshao, WANG Zitang, KUANG Zheng, et al. Experimental study on the mitigation effects of confined-blast loading[J]. Explosion and Shock Waves, 2021, 41(6): 24-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ202106003.htm
[27]	ANDERSON C E, BAKER W E, WAUTERS D K, et al. Quasi-static pressure, duration, and impulse for explosions in structures[J]. International Journal of Mechanical Sciences, 1983, 25(6): 455-464.
[28]	刘欣, 顾文彬, 蔡星会, 等. 圆柱形爆炸容器的内壁爆炸载荷[J]. 爆炸与冲击, 2022, 42(2): 19-30. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ202202002.htm LIU Xin, GU Wenbin, CAI Xinghui, et al. Blast loads on the inner wall of cylindrical explosion containment vessel[J]. Explosion and Shock Waves, 2022, 42(2): 19-30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ202202002.htm
[29]	徐景林, 顾文彬, 刘建青, 等. 圆柱形爆炸容器内爆炸载荷的分布规律[J]. 振动与冲击, 2020, 39(18): 276-282. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202018038.htm XU Jinglin, GU Wenbin, LIU Jianqing, et al. Distribution of blast loading in cylindrical explosive containment vessels[J]. Journal of Vibration and Shock, 2020, 39(18): 276-282. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ202018038.htm
[30]	周清. 密闭空间内爆炸引起的内壁超压分布规律及简化计算研究[D]. 硕士学位论文. 天津: 天津大学, 2008. ZHOU Qing. Study on distribution law and simplified calculation of inner wall overpressure caused by explosion in confined space[D]. Master Thesis. Tianjin: Tianjin University, 2008. (in Chinese)
[31]	陈鹏宇, 侯海量, 金键, 等. 舰船舱内爆炸载荷简化载荷计算模型[J]. 舰船科学技术, 2020, 42(17): 22-29. https://www.cnki.com.cn/Article/CJFDTOTAL-JCKX202017006.htm CHEN Pengyu, HOU Hailiang, JIN Jian, et al. Simplified calculation model for explosion loading in ship cabin[J]. Ship Science and Technology, 2020, 42(17): 22-29. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JCKX202017006.htm
[32]	侯日立, 周平, 彭建祥. 冲击波作用下LY12铝合金结构毁伤的数值模拟[J]. 爆炸与冲击, 2012, 32(5): 470-474. https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201205005.htm HOU Rili, ZHOU Ping, PENG Jianxiang. Numerical simulation of shock damage of LY12 aluminium alloy structure[J]. Explosion and Shock Waves, 2012, 32(5): 470-474. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201205005.htm