多再入工况下一体化热防护系统拓扑优化设计

邓通相; 匡格平; 胡兆财; 唐光武; 杨强; 高博

doi:10.21656/1000-0887.440163

多再入工况下一体化热防护系统拓扑优化设计

doi: 10.21656/1000-0887.440163

1.
哈尔滨工业大学复合材料与结构研究所，哈尔滨 150001
2.
北京宇航系统工程研究所，北京 100076
3.
招商局重庆交通科研设计院有限公司桥梁工程结构动力学国家重点实验室，重庆 400067

(我刊编委唐光武来稿)

基金项目:

国家自然科学基金项目 11672088

国家自然科学基金项目 11472092

国家自然科学基金项目 11502058

国家自然科学基金项目 12090034

中国科协青年人才托举工程 2021QNRC001

详细信息

作者简介:
邓通相(1998—)，男，硕士(E-mail: 21s018013@stu.hit.edu.cn)

通讯作者:
高博(1992—)，男，助理教授，博士(通讯作者. E-mail: 18b918033@stu.hit.edu.cn)

中图分类号: O34;V45
计量
- 文章访问数: 478
- HTML全文浏览量: 138
- PDF下载量: 60
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-29
- 修回日期: 2023-06-21
- 刊出日期: 2023-11-01

Topology Optimizations of Integrated Thermal Protection Systems in Multiple Reentry Load Cases

1.
Center for Composite Materials and Structure, Harbin Institute of Technology, Harbin 150001, P.R.China
2.
Beijing Institute of Astronautical Systems Engineering, Beijing 100076, P.R.China
3.
State Key Laboratory of Bridge Engineering Structural Dynamics, China Merchants Chongqing Communications Technology Research & Design Institute Co., Ltd., Chongqing 400067, P.R.China

(Contributed by TANG Guangwu, M. AMM Editorial Board)

摘要

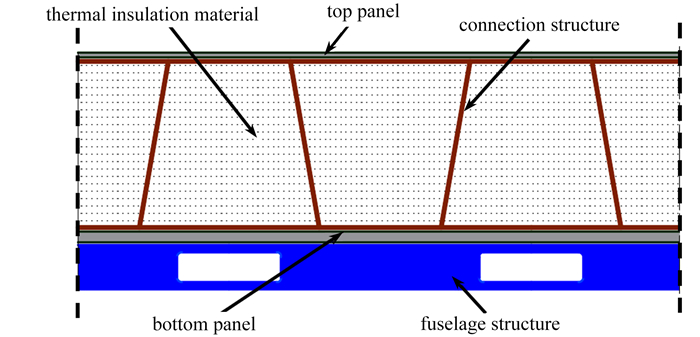
摘要: 一体化热防护系统(integrated thermal protection system, ITPS)需要同时满足承载与隔热的需求. 以波纹夹芯方案的ITPS为例，这需要其连接结构具有较高的力学性能与较低的热导率. 而再入环境的工况恶劣，如何合理地设计连接结构是ITPS性能提升的关键. 为解决这一问题，综合考虑了再入过程中气动热载荷最大时刻和气动压力载荷最大时刻对应的两种极端工况，以应变能和净传热速率的最小化作为目标函数，将质量作为约束条件，对ITPS的连接结构进行了拓扑优化. 随后对拓扑优化得到的构型重新建模并进行了热力耦合分析. 结果表明，拓扑优化得到的连接结构与文献中的初始波纹夹芯构型和单一工况下拓扑优化得到的构型相比，上面板的最大位移、下面板的温度和质量均有效降低. 由于材料用量的减少和结构复杂度的增加，连接结构在应力水平上有所增加，但仍满足使用需求. 这表明了考虑多再入工况的拓扑优化策略可以有效提升ITPS的刚度与隔热能力，缓解结构的热短路效应. 随着增材制造等相关技术的发展，拓扑优化在ITPS的连接结构以及其他的热结构设计中具有广阔的前景.
- 一体化热防护系统 /
- 拓扑优化 /
- 多工况 /
- 热力耦合
Abstract: The integrated thermal protection system (ITPS) needs to meet both load-bearing and heat-insulating requirements. In terms of the ITPS with a corrugated sandwich structure, this requires the connection structure of the ITPS to have high mechanical properties with low thermal conductivity. However, the re-entry environment is severe, how to reasonably design the connection structure is key to improve the performances of the ITPS. To solve this problem, 2 extreme load conditions corresponding to the maximum aerodynamic heat load and the maximum aerodynamic pressure load during the reentry process were comprehensively considered, the objective function was constructed with the minimized strain energy and the net heat transfer rate, the mass was used as a constraint, and the topology optimization of the ITPS connection structure was carried out. Then, the configuration obtained through the topology optimization was reconstructed and the thermal mechanical coupling analysis was carried out. The results show that, the maximum displacement of the top panel, the temperature of the bottom panel and the mass of the optimized connection structure were reduced effectively compared with those of the initial corrugated sandwich configuration and the topology optimization configuration in single load cases in the literatures. Due to the reduction of material consumption and the increase of the structural complexity, the stress level of the connection structure increases, but it still meets the requirements of use. This means that, the topology optimization strategy considering multiple reentry load cases can effectively improve the stiffness and the insulation capacity of the ITPS and alleviate the thermal short-circuiting of the structure. With the development of additive manufacturing and other related technologies, the topology optimization method has broad prospects in the design of the connection structures for the ITPS and other thermal structures.
- integrated thermal protection system /
- topology optimization /
- multiple load cases /
- thermo-mechanical coupling
edited-by

edited-by
注释:

1) (我刊编委唐光武来稿)

HTML全文

图 1 典型的ITPS结构

Figure 1. A typical ITPS structure

下载: 全尺寸图片幻灯片

图 2 ITPS的几何模型

Figure 2. Geometric characteristics of the ITPS

下载: 全尺寸图片幻灯片

图 3 典型的再入环境载荷

Figure 3. Typical aerodynamic loads during the re-entry flight

下载: 全尺寸图片幻灯片

图 4 ITPS的设计域和边界条件

Figure 4. The design domain and boundary conditions of the ITPS

下载: 全尺寸图片幻灯片

图 5 不同权重组合下的拓扑优化构型

Figure 5. Topology optimized configurations under different weight combinations

下载: 全尺寸图片幻灯片

图 6 模型重建后的构型特征

Figure 6. Configurational characteristics after model reconstruction

下载: 全尺寸图片幻灯片

图 7 文献[8]中的拓扑优化构型特征

Figure 7. Topology optimized configuration characteristics in ref. [8]

下载: 全尺寸图片幻灯片

图 8 拓扑优化构型与参考构型的热力响应对比

Figure 8. Comparison of thermal and mechanical responses between topology optimized configurations with reference configurations

下载: 全尺寸图片幻灯片

图 9 ITPS连接结构温度响应

Figure 9. Temperature response of the connection structure of the ITPS

下载: 全尺寸图片幻灯片

表 1 ITPS的尺寸参数

Table 1. Sizes of the referenced ITPS design

parameter	value	parameter	value
t_T/mm	2.1	h/mm	120.0
t_W/mm	3.1	L/mm	117.0
t_B/mm	5.3	θ/(°)	71.0

下载: 导出CSV

表 2 材料性能参数

Table 2. Material properties

material	Inconel 718	TC4	Al 2024	Saffil
density ρ/(kg/m³)	8 100	4 440	2 770	50
elastic modulus E/GPa	199(393 K) 153(1 033 K)	115	71	-
Poisson’s ratio μ	0.294	0.3	0.33	-
thermal expansion coefficient α/K^-1	1.26×10^-5(373 K) 1.61×10^-5(1 033 K)	9.6×10^-6	2.0×10^-5	-
thermal conductivity k/(W/(m·K))	11.1(293 K) 28(1 273 K)	7.6	816(255 K) 975(477 K)	0.014(477 K) 0.154(1 144 K)
specific heat c/(J/kg)	432(293 K) 620(1 070 K)	560	944	942(389 K) 1 339(1 170 K)

下载: 导出CSV

表 3 优化构型与参考构型的结构响应对比

Table 3. Comparison of structural responses between optimized configurations with reference configurations

	ref #1	ref #2	opt #1	opt #2
D_{T, max}/mm	5.16	2.97	1.90	1.87
T_{B, max}/K	393.20	346.38	333.57	328.33
S_{T, max}/MPa	579.61	289.36	327.80	312.99
S_{W, max}/MPa	291.90	353.02	384.11	383.51
S_{B, max}/MPa	199.30	52.43	99.67	88.38
V_f	0.045 2	0.045 1	0.032 0	0.029 0

下载: 导出CSV

参考文献(34)

[1]	WEI K, HE R J, CHENG X M, et al. Fabrication and mechanical properties of lightweight ZrO₂ ceramic corrugated core sandwich panels[J]. Materials & Design, 2014, 64: 91-95.
[2]	郑辉, 邱雷, 袁慎芳, 等. C/C热防护结构高温气流损伤导波监测实验方法[J]. 航空学报, 2022, 43(8): 428-440. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202208031.htm ZHENG Hui, QIU Lei, YUAN Shenfang, et al. Research on guided wave monitoring experimental method for high temperature airflow damage of C/C thermal protection structures[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(8): 428-440. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB202208031.htm
[3]	BAPANAPALLI S K, MARTINEZ O, GOGU C, et al. Analysis and design of corrugated-core sandwich panels for thermal protection system of space vehicles[C]// 47th AIAA Structures, Structural Dynamics and Materials Conference, Newport, American Institute of Aeronautics and Astronautics. Newport, Rhode Island, 2006.
[4]	WEI K, CHENG X M, MO F H, et al. Design and analysis of integrated thermal protection system based on lightweight C/SiC pyramidal lattice core sandwich panel[J]. Materials & Design, 2016, 111: 435-444.
[5]	LIANG H, WANG Y, TONG M, et al. Multi-scale strength analysis of bolted connections used in integral thermal protection system[J]. Chinese Journal of Aeronautics, 2018, 31(8): 1728-1740. doi: 10.1016/j.cja.2018.06.007
[6]	杨亚政, 杨嘉陵, 方岱宁. 高超声速飞行器热防护材料与结构的研究进展[J]. 应用数学和力学, 2008, 29(1): 47-56. http://www.applmathmech.cn/article/id/1021 YANG Yazheng, YANG Jialing, FANG Daining. Research progress of thermal protection materials and structures for hypersonic vehicles[J]. Applied Mathematics and Mechanics, 2008, 29(1): 47-56. (in Chinese) http://www.applmathmech.cn/article/id/1021
[7]	LE V T, HA N S, GOO N S. Advanced sandwich structures for thermal protection systems in hypersonic vehicles: a review[J]. Composites(Part B): Engineering, 2021, 226: 109301. doi: 10.1016/j.compositesb.2021.109301
[8]	YANG Q, GAO B, XU Z Y, et al. Topology optimisations for integrated thermal protection systems considering thermo-mechanical constraints[J]. Applied Thermal Engineering, 2019, 150: 995-1001. doi: 10.1016/j.applthermaleng.2019.01.067
[9]	彭世彬, 郭瑞, 冯上升, 等. 主动冷却点阵夹层防热结构温度响应计算模型[J]. 应用数学和力学, 2022, 43(5): 477-489. doi: 10.21656/1000-0887.420405 PENG Shibin, GUO Rui, FENG Shangsheng, et al. A calculation model for temperature responses of active cooling lattice sandwich structures for thermal protection[J]. Applied Mathematics and Mechanics, 2022, 43(5): 477-489. (in Chinese) doi: 10.21656/1000-0887.420405
[10]	王琪, 吉庭武, 谢公南, 等. 轻质热防护系统波纹夹芯结构热力耦合分析[J]. 应用数学和力学, 2013, 34(2): 172-182. doi: 10.3879/j.issn.1000-0887.2013.02.007 WANG Qi, JI Tingwu, XIE Gongnan, et al. Thermal-mechanical coupling analysis of corrugated sandwich structure of lightweight thermal protection system[J]. Applied Mathematics and Mechanics, 2013, 34(2): 172-182. (in Chinese) doi: 10.3879/j.issn.1000-0887.2013.02.007
[11]	CHEN Y, ZHANG L, HE C, et al. Thermal insulation performance and heat transfer mechanism of C/SiC corrugated lattice core sandwich panel[J]. Aerospace Science and Technology, 2021, 111: 106539. doi: 10.1016/j.ast.2021.106539
[12]	SHI S B, DAI C X, WANG Y F. Design and optimization of an integrated thermal protection system for space vehicles[C]// 20th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Glasgow, American Institute of Aeronautics and Astronautics. Glasgow, Scotland, 2015: 3553.
[13]	XIE G, WANG Q, SUNDEN B, et al. Thermomechanical optimization of lightweight thermal protection system under aerodynamic heating[J]. Applied Thermal Engineering, 2013, 59(1/2): 425-434.
[14]	YANG Q, MENG S H, XIE W H, et al. Effective mitigation of the thermal short and expansion mismatch effects of an integrated thermal protection system through topology optimization[J]. Composites(Part B): Engineering, 2017, 118: 149-157. doi: 10.1016/j.compositesb.2017.03.038
[15]	JIANG F, YE Z, YU W, et al. Analysis of reusable integrated thermal protection panel elements with various insulating core options[C]// 55th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Maryland, American Institute of Aeronautics and Astronautics. National Harbor, Maryland, 2014: 0351.
[16]	DEATON J D, GRANDHI R V. Stiffening of restrained thermal structures via topology optimization[J]. Structural and Multidisciplinary Optimization, 2013, 48(4): 731-745. doi: 10.1007/s00158-013-0934-5
[17]	DEATON J D, GRANDHI R V. Stress-based design of thermal structures via topology optimization[J]. Structural and Multidisciplinary Optimization, 2016, 53(2): 253-270.
[18]	TAKEZAWA A, YOON G H, JEONG S H, et al. Structural topology optimization with strength and heat conduction constraints[J]. Computer Methods in Applied Mechanics & Engineering, 2014, 276: 341-361.
[19]	ZHANG W, YANG J, XU Y, et al. Topology optimization of thermoelastic structures: mean compliance minimization or elastic strain energy minimization[J]. Structural and Multidisciplinary Optimization, 2014, 49(3): 417-429.
[20]	WANG B, YAN J, CHENG G. Optimal structure design with low thermal directional expansion and high stiffness[J]. Engineering Optimization, 2011, 43(6): 581-595.
[21]	YANG Z H, ZHANG Y C, LIU S T, et al. Microstructural topology optimization for patch-based sandwich panel with desired in-plane thermal expansion and structural stiffness[J]. Structural and Multidisciplinary Optimization, 2021, 64(2): 779-795.
[22]	KIM W, GRANDHI R V, HANEY M. An evolutionary optimization method for designing a thermal protection system for dynamics[J]. Mechanics Based Design of Structures and Machines, 2006, 34(1): 1-24.
[23]	KIM W, GRANDHI R V, HANEY M. Multi-objective evolutionary optimization method for thermal protection system design[C]// 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Austin, American Institute of Aeronautics and Astronautics. Austin, Texas, 2005: 2311.
[24]	PENMETSA R C, GRANDHI R V, HANEY M. Topology optimization for an evolutionary design of a thermal protection system[J]. AIAA Journal, 2012, 44(11): 2663-2671.
[25]	XU Q, LI S, MENG Y. Optimization and re-design of integrated thermal protection systems considering thermo-mechanical performance[J]. Applied Sciences, 2021, 11(15): 6916.
[26]	杨强. 一体化热防护系统设计与综合效能评估方法研究[D]. 硕士学位论文. 哈尔滨: 哈尔滨工业大学, 2013. YANG Qiang. Design and performance evaluation method of integrated thermal protection systems[D]. Master Thesis. Harbin: Harbin Institute of Technology, 2013. (in Chinese)
[27]	杜鹏. 大型箱体结构拓扑优化设计研究[D]. 硕士学位论文. 郑州: 郑州大学, 2016. DU Peng. A research on topology optimization design of large-scale box structure[D]. Master Thesis. Zhengzhou: Zhengzhou University, 2016. (in Chinese)
[28]	叶红玲, 隋允康. 基于ICM方法三维连续体结构拓扑优化[J]. 固体力学学报, 2006, 27(4): 387-393. https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX200604010.htm YE Hongling, SUI Yunkang. ICM based topological optimization of 3D continuum structure[J]. Chinese Journal of Solid Mechanics, 2006, 27(4): 387-393. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX200604010.htm
[29]	方子帆, 杨磊, 杜道佳, 等. 支撑结构多目标拓扑优化设计研究[J]. 中国机械工程, 2010, 21(15): 1836-1839. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJX201015018.htm FANG Zifan, YANG Lei, DU Daojia, et al. Research on topology optimization design for support structure[J]. Chinese Mechanical Engineering, 2010, 21(15): 1836-1839. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGJX201015018.htm
[30]	BENDSØE M P, SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of Applied Mechanics, 1999, 69(9/10): 635-654.
[31]	MYERS D E, MARTIN C J, BLOSSER M L. Parametric weight comparison of current and proposed thermal protection system (TPS) concepts[C]// 33rd Thermophysics Conference, Norfolk, American Institute of Aeronautics and Astronautics. Norfolk, VA, 1999.
[32]	KRYSKO A V, AWREJCEWICZ J, PAVLOV S P, et al. Topological optimization of thermoelastic composites with maximized stiffness and heat transfer[J]. Composites(Part B): Engineering, 2019, 158: 319-327.
[33]	SVANBERG K. A class of globally convergent optimization methods based on conservative convex separable approximations[J]. SIAM Journal on Optimization, 2002, 12(2): 555-573.
[34]	钛及钛合金棒材: GB/T 2965—2007[S]. 北京: 中国标准出版社, 2007. Titanium and titanium alloy bars: GB/T 2965—2007[S]. Beijing: Standards Press of China, 2007. (in Chinese)