求解两区域变分不等式的自适应交替方向乘子法

袁星月; 崔席勇; 冉瑞生; 张守贵

doi:10.21656/1000-0887.450171

求解两区域变分不等式的自适应交替方向乘子法

doi: 10.21656/1000-0887.450171

1.
重庆师范大学数学科学学院，重庆 401331
2.
中冶赛迪信息技术(重庆)有限公司，重庆 401120
3.
重庆师范大学计算机与信息科学学院，重庆 401331

基金项目:

国家自然科学基金 11971085

详细信息

作者简介:
袁星月(2000—), 女, 硕士生(E-mail: 2505944022@qq.com)

通讯作者:
张守贵(1973—), 男, 教授, 博士, 硕士生导师(通讯作者. E-mail: shgzhang@cqnu.edu.cn)

中图分类号: O241.82
计量
- 文章访问数: 4
- HTML全文浏览量: 3
- PDF下载量: 0
- 被引次数: 0
出版历程
- 收稿日期: 2024-06-11
- 修回日期: 2024-11-09
- 网络出版日期: 2025-07-30
- 刊出日期: 2025-07-01

A Self-Adaptive Alternating Direction Multiplier Method for Variational Inequality in 2 Domains

1.
School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, P.R.China
2.
CISDI Information Technology (Chongqing) Co., Ltd., Chongqing 401120, P.R.China
3.
School of Computer and Information Science, Chongqing Normal University, Chongqing 401331, P.R.China

摘要

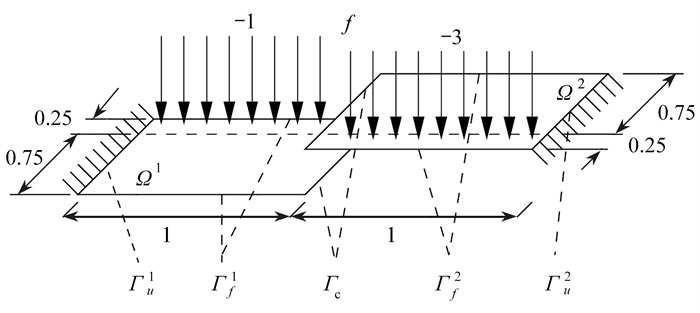
摘要: 针对一类定义在两个区域的接触问题，提出了求其数值解的自适应交替方向乘子法. 由该两区域的变分问题，得到一个由不等式约束的极小值问题，通过引入接触边界上的辅助变量得到等价的鞍点问题. 采用交替方向乘子法求鞍点问题的数值解，每次迭代依次求解显式的辅助变量、一个线性问题及更新Lagrange乘子. 基于自适应法则及迭代函数自动选取罚参数，从而提出了自适应交替方向乘子法. 证明了算法的收敛性，算例的数值结果展示了所给算法的有效性.
- 变分不等式 /
- 鞍点问题 /
- 交替方向乘子法 /
- 自适应罚参数
Abstract: A self-adaptive alternating direction multiplier method was proposed for a class of contact problems defined in 2 domains. A minimization problem constrained by inequalities was obtained for the variational problem in 2 domains, then the problem was equivalent to a saddle-point problem through introduction of an auxiliary unknown on the contact boundary. The alternating direction multiplier method was applied to the saddle point problem for the numerical solution, with each iteration successively determining the auxiliary variable explicitly, solving a linear problem and updating the Lagrange multiplier. The self-adaptive alternating direction multiplier method was proposed to select the penalty parameter automatically, by means of a self-adaptive rule and iterative functions. The results prove the convergence and demonstrate the effectiveness of the proposed method.
- variational inequality /
- saddle point problem /
- alternating direction multiplier method /
- self-adaptive penalty parameter

HTML全文

图 1 模型问题的区域

Figure 1. The domain of the model problem

下载: 全尺寸图片幻灯片

图 2 接触边界Γ_c上∂u₂/∂n₂及u_m的数值解

Figure 2. Numerical solutions of ∂u₂/∂n₂ and u_m on Γ_c

下载: 全尺寸图片幻灯片

表 1 3种算法的CPU运行时间

Table 1. CPU time for each method

ρ	SSNM			ADMM			SADMM
ρ	h=1/20	h=1/40	h=1/80	h=1/20	h=1/40	h=1/80	h=1/20	h=1/40	h=1/80
1	0.844 4	1.879 3	3.967 4	5.990 2	19.635 7	86.211 5	0.458 2	0.878 8	2.095 3
10	0.910 3	1.600 1	5.278 4	>24.688 9	>53.579 2	>121.349 8	0.452 4	0.899 6	2.032 1
10²	0.936 4	1.838 3	5.435 9	>25.859 4	>54.146 4	>115.774 4	0.494 3	1.016 8	2.262 3
10³	0.933 2	1.858 6	5.506 8	>25.991 1	>52.625 0	>117.524 3	0.545 8	1.076 1	2.500 6
10⁴	0.898 4	1.729 7	5.546 1	>26.809 8	>53.330 9	>127.610 5	0.545 2	1.054 3	2.384 3

下载: 导出CSV

表 2 3种算法的迭代次数

Table 2. The numbers of iterations for each method

ρ	SSNM			ADMM			SADMM
ρ	h=1/20	h=1/40	h=1/80	h=1/20	h=1/40	h=1/80	h=1/20	h=1/40	h=1/80
1	56	70	71	477	783	1 460	44	47	58
10	70	61	94	-	-	-	45	49	59
10²	72	67	97	-	-	-	50	53	63
10³	72	68	97	-	-	-	54	58	71
10⁴	72	68	97	-	-	-	55	57	69

下载: 导出CSV

参考文献(20)

[1]	TANG W J, HU H Y, SHEN L J. On the coupling of boundary integral and finite element methods for Signorini problems[J]. Journal of Computational Mathematics, 1998, 16 (6): 561-570.
[2]	DOSTÁL Z, NETO F A M G G, SANTOS S A. Duality-based domain decomposition with natural coarse-space for variational inequalities[J]. Journal of Computational and Applied Mathematics, 2000, 126 (1/2): 397-415.
[3]	DOSTÁL Z, HORÁK D. Theoretically supported scalable FETI for numerical solution of variational inequalities[J]. SIAM Journal on Numerical Analysis, 2007, 45 (2): 500-513.
[4]	PENG Z Y, LI D, ZHAO Y, et al. An accelerated subgradient extragradient algorithm for solving bilevel variational inequality problems involving non-Lipschitz operator[J]. Communications in Nonlinear Science and Numerical Simulation, 2023, 127 : 107549.
[5]	PENG Z Y, PENG Z Y, CAI G, et al. Inertial subgradient extragradient method for solving pseudomonotone variational inequality problems in Banach spaces[J]. Applicable Analysis, 2024, 103 (10): 1769-1789.
[6]	DOSTÁL Z, HORÁK D, STEFANICA D. A scalable FETI-DP algorithm for a semi-coercive variational inequality[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196 (8): 1369-1379.
[7]	DOSTÁL Z, HORÁK D, STEFANICA D. A scalable FETI-DP algorithm with non-penetration mortar conditions on contact interface[J]. Journal of Computational and Applied Mathematics, 2009, 231 (2): 577-591.
[8]	DOSTÁL Z, HORÁK D, KRUŽÍK J, et al. Highly scalable hybrid domain decomposition method for the solution of huge scalar variational inequalities[J]. Numerical Algorithms, 2022, 91 (2): 773-801.
[9]	LEE J. Two domain decomposition methods for auxiliary linear problems of a multibody elliptic variational inequality[J]. SIAM Journal on Scientific Computing, 2013, 35 (3): A1350-A1375.
[10]	BOUCHALA J, DOSTÁL Z, SADOWSKÁ M. Theoretically supported scalable BETI method for variational inequalities[J]. Computing, 2008, 82 (1): 53-75.
[11]	IKRAM B, SAMIRA S. Generalized Schwarz algorithm for a class of variational inequalities[J]. Applied Mathematics & Information Sciences, 2021, 15 (1): 9-15.
[12]	CHORFI A, KOKO J. Alternating direction method of multiplier for the unilateral contact problem with an automatic penalty parameter selection[J]. Applied Mathematical Modelling, 2020, 78 : 706-723.
[13]	KOKO J. Uzawa block relaxation domain decomposition method for a two-body frictionless contact problem[J]. Applied Mathematics Letters, 2009, 22 (10): 1534-1538.
[14]	ZHANG S G, GUO N X. Uzawa block relaxation method for free boundary problem with unilateral obstacle[J]. International Journal of Computer Mathematics, 2021, 98 (4): 671-689.
[15]	GLOWINSKI R. Variational Methods for the Numerical Solution of Nonlinear Elliptic Problems[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2015.
[16]	王霄婷, 龙宪军, 彭再云. 求解非单调变分不等式的一种二次投影算法[J]. 应用数学和力学, 2022, 43 (8): 927-934. doi: 10.21656/1000-0887.420414 WANG Xiaoting, LONG Xianjun, PENG Zaiyun. A double projection algorithm for solving non-monotone variational inequalities[J]. Applied Mathematics and Mechanics, 2022, 43 (8): 927-934. (in Chinese) doi: 10.21656/1000-0887.420414
[17]	张霖森, 程兰, 张守贵. 曲率障碍下四阶变分不等式的交替方向乘子法[J]. 应用数学和力学, 2023, 44 (5): 595-604. doi: 10.21656/1000-0887.430243 ZHANG Linsen, CHENG Lan, ZHANG Shougui. An alternating direction multiplier method for 4th-order variational inequalities with curvature obstacle[J]. Applied Mathematics and Mechanics, 2023, 44 (5): 595-604. (in Chinese) doi: 10.21656/1000-0887.430243
[18]	袁欣, 张守贵. 无摩擦弹性接触问题的自适应交替方向乘子法[J]. 应用数学和力学, 2023, 44 (8): 989-998. doi: 10.21656/1000-0887.440079 YUAN Xin, ZHANG Shougui. A self-adaptive alternating direction multiplier method for frictionless elastic contact problems[J]. Applied Mathematics and Mechanics, 2023, 44 (8): 989-998. (in Chinese) doi: 10.21656/1000-0887.440079
[19]	王欣, 郭科. 一类非凸优化问题广义交替方向法的收敛性[J]. 应用数学和力学, 2018, 39 (12): 1410-1425. WANG Xin, GUO Ke. Convergence of the generalized alternating direction method of multipliers for a class of nonconvex optimization problems[J]. Applied Mathematics and Mechanics, 2018, 39 (12): 1410-1425. (in Chinese)
[20]	ZHANG S G, YAN Y Y, RAN R S. Path-following and semismooth Newton methods for the variational inequality arising from two membranes problem[J]. Journal of Inequalities and Applications, 2019, 2019 (1): 1.