Topology Optimization of Nonlinear Material Structures Based on Parameterized Level Set and Substructure Methods
-
摘要: 针对利用传统水平集法进行非线性结构拓扑优化计算过程复杂及计算效率低等问题,将参数化水平集方法引入材料非线性结构拓扑优化中。通过全局径向基函数插值初始水平集函数,建立了以插值系数为设计变量、结构的应变能最小为目标函数、材料用量为约束条件的材料非线性结构拓扑优化模型,利用有限元分析对材料非线性结构建立平衡方程,并用迭代法求解。同时,采用子结构法划分设计区域为若干个子区域,将全自由度平衡方程的求解分解为缩减的平衡方程和多个子结构内部位移的求解,减小了计算成本。算例表明,这种处理非线性关系的方法可以在保证数值稳定的同时提高计算效率,得到边界清晰、结构合理的拓扑优化构形。Abstract: In order to overcome the problems of complicated calculation process and lower computational efficiency of the traditional level set method (LSM), for nonlinear structure topology optimization, a parameterized level set method (PLSM) was introduced. Through interpolation of the initial level set function with the globally supported radial basis function (GSRBF), a nonlinear material structure topology optimization model was established with the interpolation coefficient as the design variable, the minimum strain energy of the structure as the objective function, and the material amount as the constraint condition. The equilibrium equation for the nonlinear material structure was established by finite element analysis, and solved with the iterative method. In addition, the substructure method (i.e. the domain decomposition method) was used to divide the design area into several sub-areas, and the solution to the full degree of freedom equilibrium equation was decomposed into a set of solutions of reduced equilibrium equations and solutions of multiple substructures’ internal displacements, which could reduce the computation cost. Examples show that, this method can ensure the numerical stability, improve the computational efficiency, and obtain the topology optimization configuration with clear boundaries and reasonable structures.
-
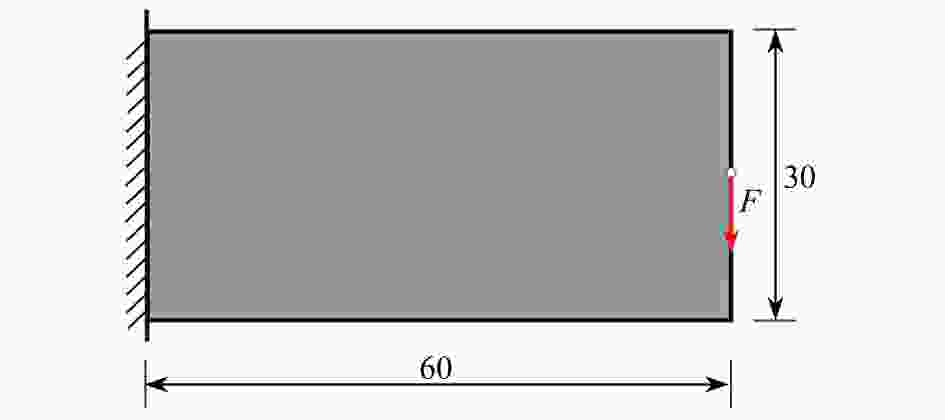
表 1 悬臂梁标准有限元法与子结构法计算结果对比
Table 1. The results of the cantilever beam standard finite element method and the substructure method
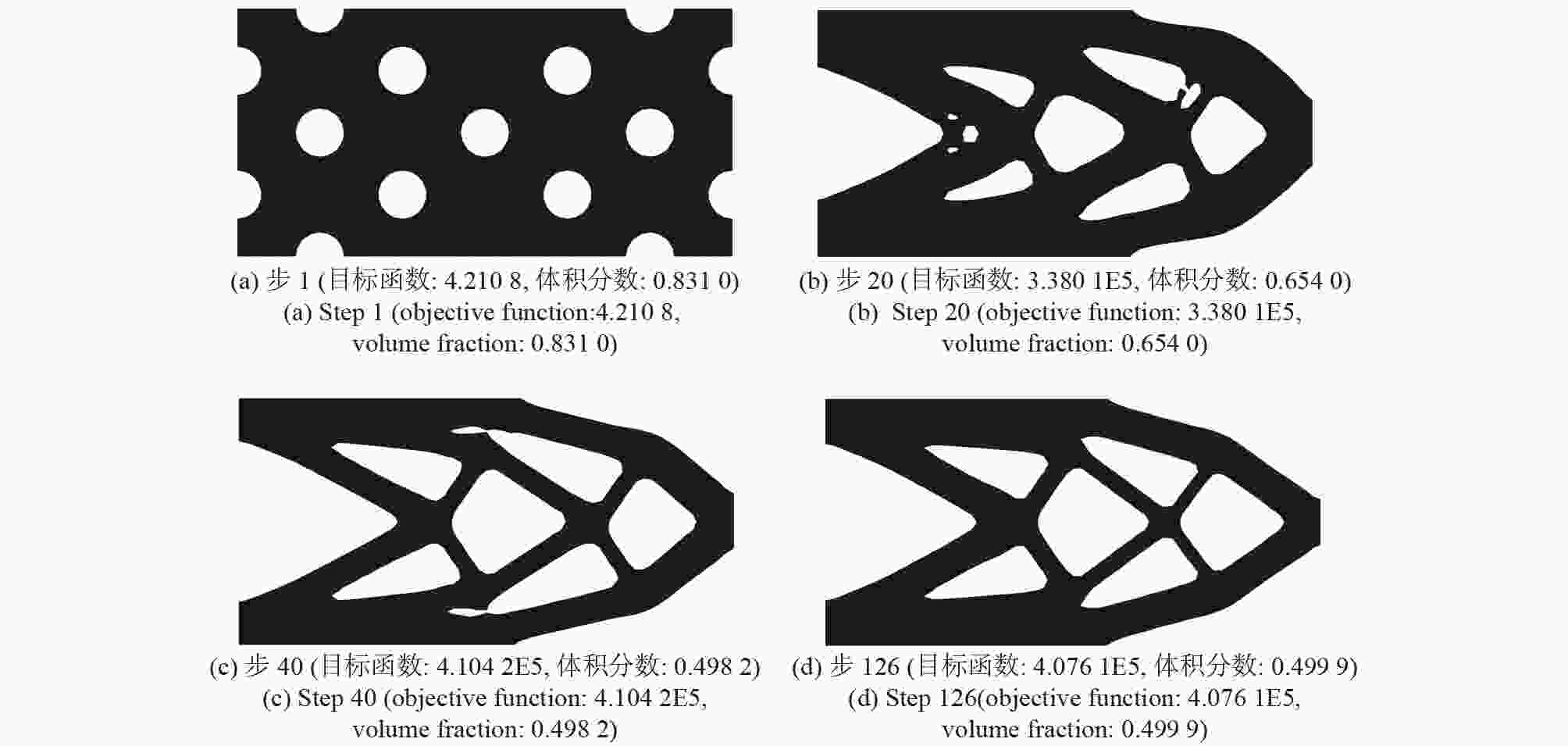
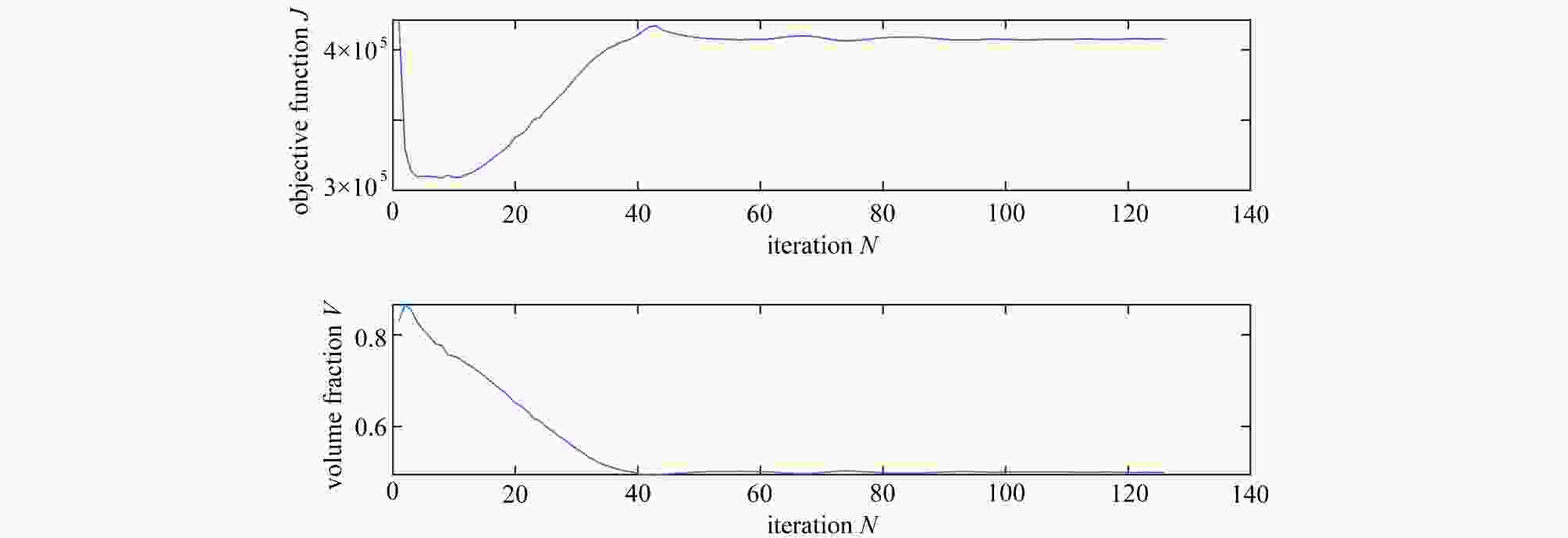
$N_{\rm{CEX}} \times N_{\rm{CEY}}$ $n_{\rm{elx}} \times n_{\rm{ely}}$ objective function J volume fraction V step time t/s optimized design standard finite element method: 60×30 4.076 1E5 0.499 9 6.014 7 
$12 \times 6$ $5 \times 5$ 4.072 7E5 0.500 3 4.937 9 
$6 \times 3$ $10 \times 10$ 4.076 1E5 0.499 8 2.736 2 
$2 \times 1$ $30 \times 30$ 4.066 5E5 0.500 3 1.336 4 
表 2 简支梁标准有限元法与子结构法计算结果对比
Table 2. The results of the freely supported beam standard finite element method and the substructure method
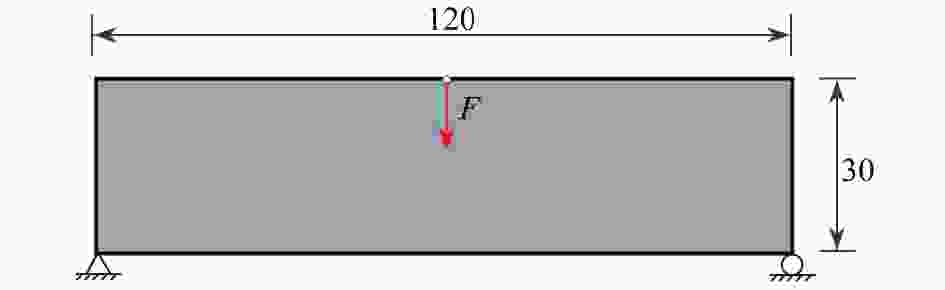
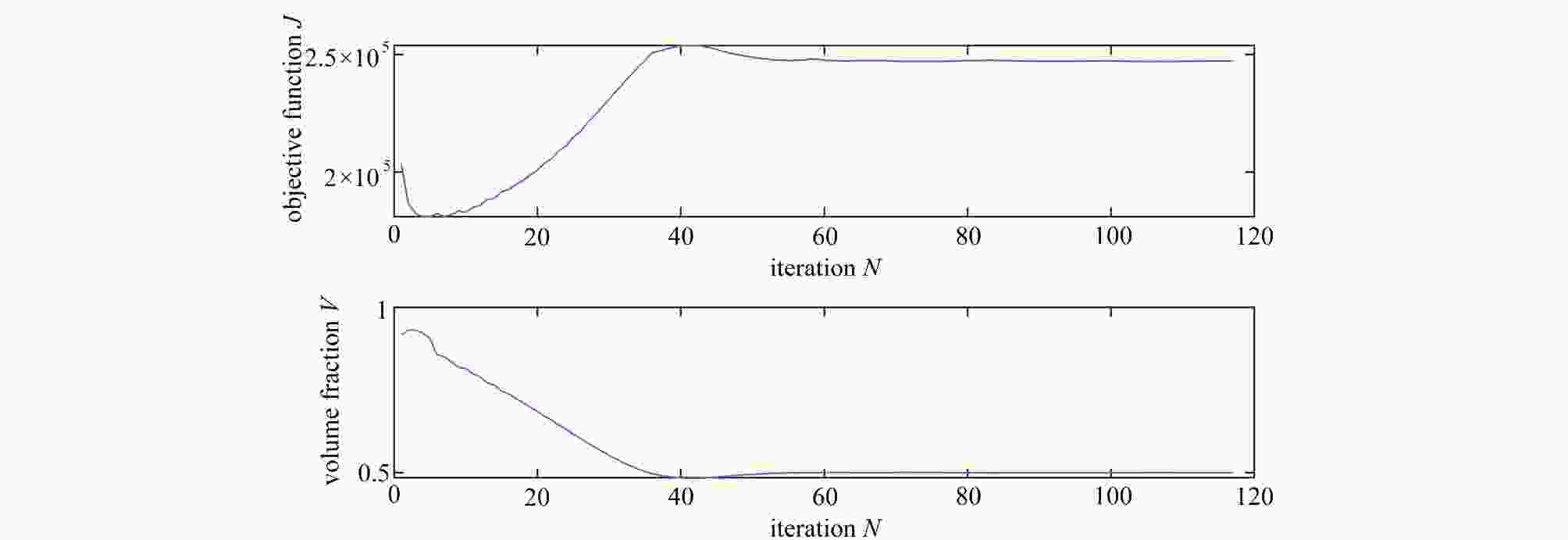
$N_{\rm{CEX}} \times N_{\rm{CEY}}$ $n_{\rm{elx}} \times n_{\rm{ely}}$ objective function J volume fraction V step time t/s optimized design standard finite element method: 120×30 2.479 7E5 0.499 9 40.358 8 
$24 \times 6$ $5 \times 5$ 2.475 5E5 0.499 9 47.779 5 
$12 \times 3$ $10 \times 10$ 2.476 4E5 0.500 3 30.279 1 
$4 \times 1$ $30 \times 30$ 2.476 3E5 0.501 0 16.701 1 
-
[1] 卫志军, 申利敏, 关晖, 等. 拓扑优化技术在抑制流体晃荡中的数值模拟研究[J]. 应用数学和力学, 2021, 42(1): 49-57. (WEI Zhijun, SHEN Limin, GUAN Hui, et al. Numerical simulation of topology optimization technique for tank sloshing suppression[J]. Applied Mathematics and Mechanics, 2021, 42(1): 49-57.(in Chinese) [2] OSHER S. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations[J]. Journal of Computational Physics, 1988, 79(1): 12-49. doi: 10.1016/0021-9991(88)90002-2 [3] WANG S, WANG M Y. Radial basis functions and level set method for structural topology optimization[J]. International Journal for Numerical Methods in Engineering, 2010, 65(12): 2060-2090. [4] WANG F, SIGMUND O, JENSEN J S. Design of materials with prescribed nonlinear properties[J]. Journal of the Mechanics and Physics of Solids, 2014, 69(2): 156-174. [5] XIA L, FRITZEN F, BREITKOPF P. Evolutionary topology optimization of elastoplastic structures[J]. Structural & Multidiplinary Optimization, 2017, 55(2): 569-581. [6] CHEN W, XIA L, YANG J, et al. Optimal microstructures of elastoplastic cellular materials under various macroscopic strains[J]. Mechanics of Materials, 2018, 118: 120-132. doi: 10.1016/j.mechmat.2017.10.002 [7] GUYAN R J. Reduction of stiffness and mass matrices[J]. AIAA Journal, 1965, 3(2): 380. doi: 10.2514/3.2874 [8] 封建湖. 三维进气道系统流场的数值模拟研究[D]. 博士学位论文. 西安: 西北工业大学, 1995FENG Jianhu. On numerical simulation of three-dimensional aircraft inlet systems[D]. PhD Thesis. Xi’an: Northwestern Polytechnical University, 1995. (in Chinese) [9] MAHDIABADI M K, BARTL A, XU D, et al. An augmented free-interface-based modal substructuring for nonlinear structural dynamics including interface reduction[J]. Journal of Sound and Vibration, 2019, 462(8): 114915. [10] ZHAO Y B, GUO W J, DUAN S H, et al. A novel substructure-based topology optimization method for the design of wing structure[J]. International Journal for Simulation & Multidisciplinary Design Optimization, 2017, 8: A5. [11] WU Z, XIA L, WANG S, et al. Topology optimization of hierarchical lattice structures with substructuring[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 345: 602-617. doi: 10.1016/j.cma.2018.11.003 [12] FU J, XIA L, GAO L, et al. Topology optimization of periodic structures with substructuring[J]. Journal of Mechanical Design, 2019, 141(7): 071403. doi: 10.1115/1.4042616 [13] DIJK N P, MAUTE K, LANGELAAR M, et al. Level-set methods for structural topology optimization[J]. Structural and Multidisciplinary Optimization, 2013, 48(3): 437-472. doi: 10.1007/s00158-013-0912-y [14] 沈亚栋. 结构拓扑优化的参数化水平集方法研究[D]. 博士学位论文. 西安: 长安大学, 2019SHEN Yadong. Research on parametric level set method for structural topology optimization[D]. PhD Thesis. Xi’an: Chang’an University, 2019. (in Chinese) [15] 王超逸, 封建湖. 拓扑优化中水平集方法的局限性及改进方法[J]. 建筑科学与工程学报, 2011, 28(2): 119-126. (WANG Chaoyi, FENG Jianhu. Weakness of level set method in topology optimization and it’s improvement[J]. Journal of Architecture and Civil Engineering, 2011, 28(2): 119-126.(in Chinese) [16] WEI P, LI Z, LI X, et al. An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions[J]. Structural & Multidisciplinary Optimization, 2018, 58(2): 831-849. [17] JUNG D, GEA H C. Topology optimization of nonlinear structures[J]. Finite Elements in Analysis & Design, 2004, 40(11): 1417-1427. [18] JUNG D, GEA H C. Compliant mechanism design with non-linear materials using topology optimization[J]. International Journal of Mechanics and Materials in Design, 2004, 1(2): 157-171. doi: 10.1007/s10999-004-1494-z [19] RAMOS A S, PAULINO G H. Filtering structures out of ground structures: a discrete filtering tool for structural design optimization[J]. Structural & Multidisciplinary Optimization, 2016, 54(1): 95-116. [20] WANG M Y, WANG X, GUO D. A level set method for structural topology optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(1): 227-246. [21] ROCKAFELLAR R T. The multiplier method of Hestenes and Powell applied to convex programming[J]. Journal of Optimization Theory & Applications, 1973, 12(6): 555-562. [22] 裴世源, 徐华. 非均质复合材料力学性能的确定性多尺度计算方法[J]. 西安交通大学学报, 2015, 49(10): 8-13. (PEI Shiyuan, XU Hua. Deterministic multiscale method for heterogeneous composite material[J]. Journal of Xi’an Jiaotong University, 2015, 49(10): 8-13.(in Chinese) doi: 10.7652/xjtuxb201510002 -




 下载:
下载:



 渝公网安备50010802005915号
渝公网安备50010802005915号