Bragg Resonance and Phase Upshift of Linear Water Waves Excited by a Finite Periodic Array of Parabolic Trenches
-
摘要:
该文解析研究了有限个周期排列的抛物形沟槽激发的水波Bragg共振。首先, 利用变量替换, 先将系数为隐函数的修正缓坡方程(MMSE)转化为系数为显函数的显式方程。然后,构造了修正缓坡方程的Frobenius级数解, 并给出了级数解的收敛条件。最后,利用质量守恒的耦合条件, 建立了反射系数的解析公式。根据反射系数的解析公式, 分析了沟槽个数、沟槽深度与宽度对Bragg共振峰值、共振相位和共振带宽的影响。当沟槽深度和宽度固定而沟槽个数增加时, 共振峰值逐渐增大并趋向于1, 而共振带宽则逐渐变窄并趋于固定值。当沟槽个数和宽度固定时, Bragg共振峰值随沟槽深度增加而增加。当沟槽个数和深度固定时, Bragg共振反射峰值随沟槽宽度增加而先增后减, 预示了沟槽存在某个宽度使得共振峰值达到最大, 为Bragg共振反射针对沟槽宽度的优化奠定了理论基础。特别地, 前不久在有限个周期排列旋轮线形沟槽上刚刚观察到的Bragg共振反射峰值相位的上移现象, 再次在该文考虑的抛物形沟槽上得到确认, 表明针对有限周期排列的沟槽地形, Bragg共振反射峰值的相位上移是一个普遍现象。也因此说明, 凡是正弦沙纹和周期人工沙坝所激发的Bragg共振反射, 其主振相位将会下移, 而凡是周期系列沟槽所激发的Bragg共振反射, 无论沟槽形状如何, 其主振相位都将上移。另外,我们从Bragg共振的原始定义出发,定量地解释了相位上移发生的数学机理。
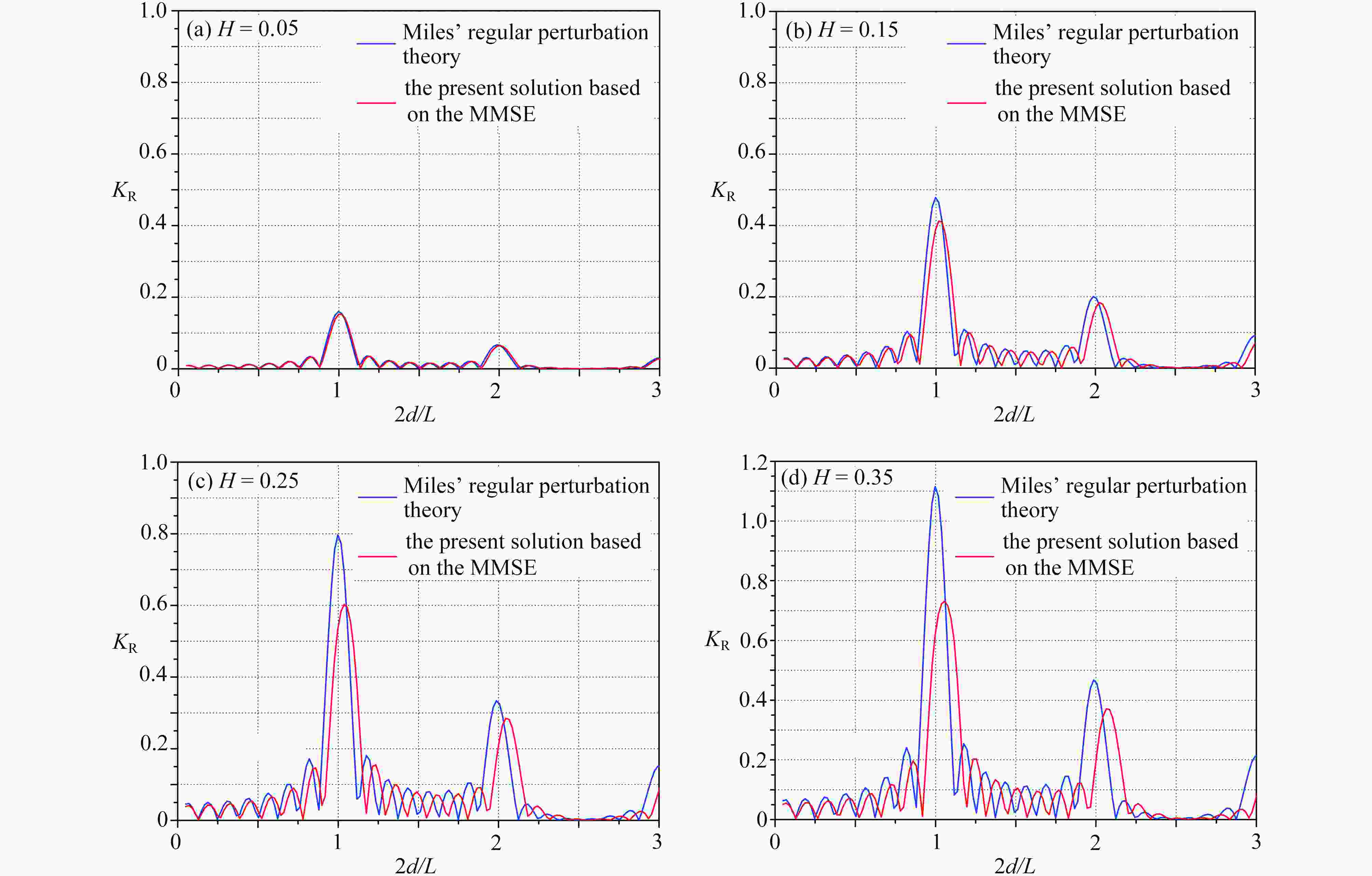
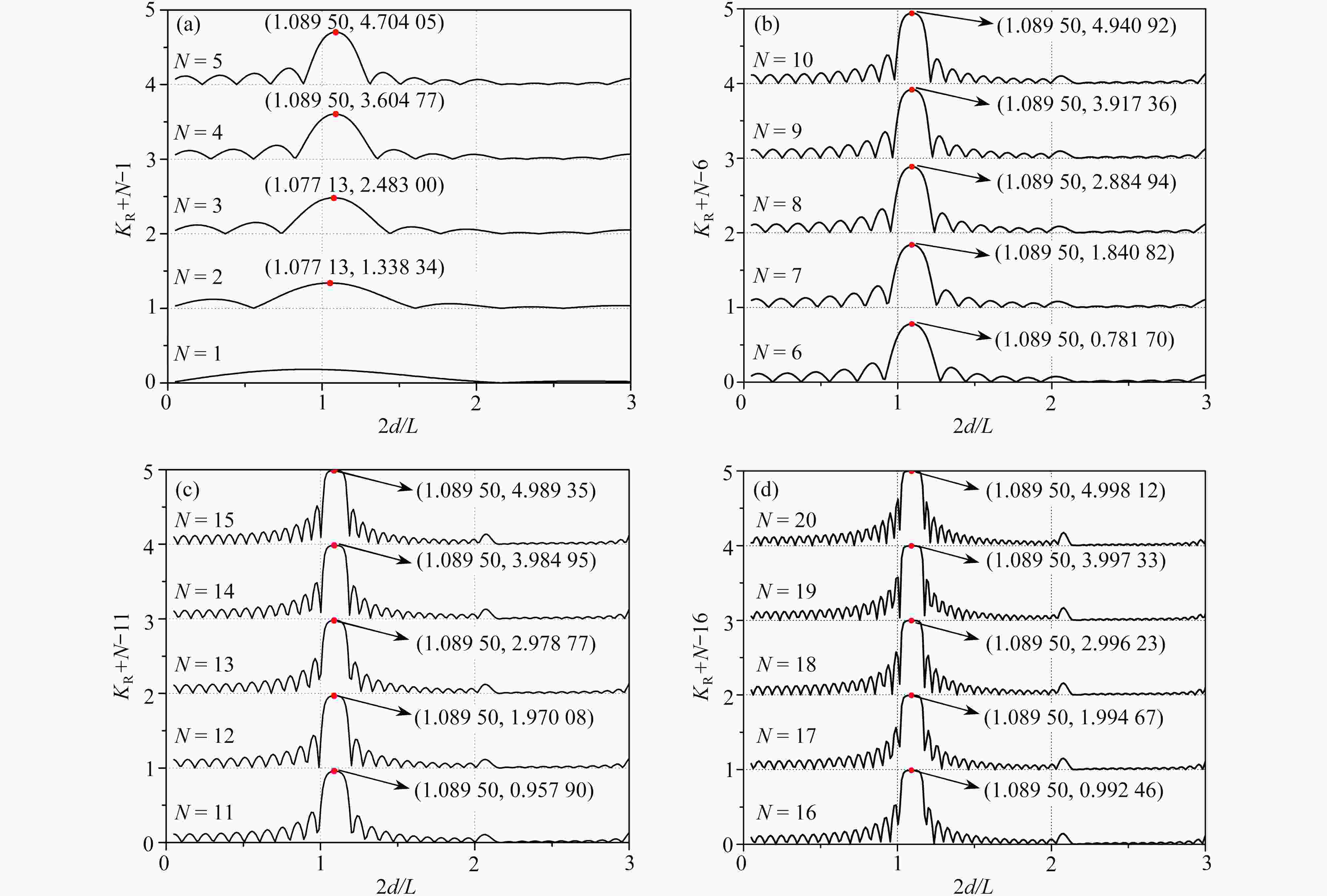
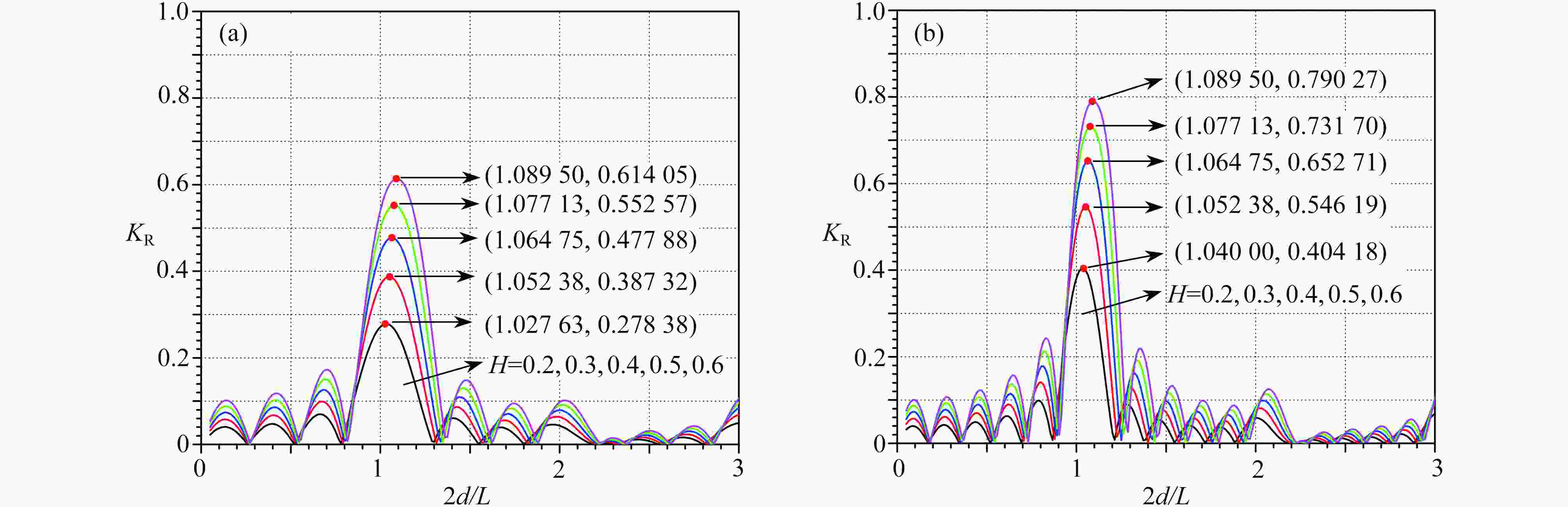
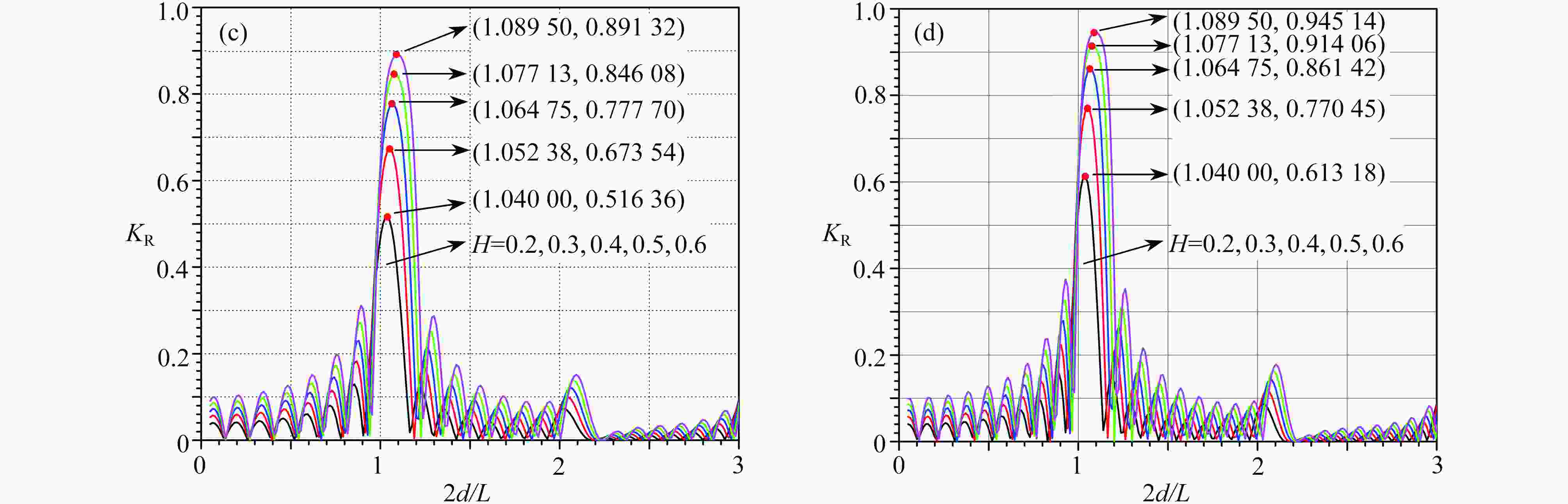
Abstract:The Bragg resonant reflection excited by a finite periodic array of parabolic trenches was analytically studied. First, the modified mild-slope equation (MMSE) with implicit coefficients was transformed into an ordinary differential equation with explicit coefficients through variable substitution. Second, an analytical solution to the MMSE was established in terms of the Frobenius series, and the convergence condition for the series solution was given. Finally, by means of the mass-conservation matching conditions, an analytical formula for the reflection coefficient was built. With the analytical formula, the effects of the number, the depth and the width of trenches on the peak value, the phase and the band width of the resonance, were investigated. The results show that, when the depth and width of trenches keep constant, and the number of trenches increases, the Bragg resonance peak value will increase up to 1, while the resonance bandwidth will narrow down and approach a fixed value. When the number and width of trenches keep constant, the Bragg resonance peak value will increase with the depth of trenches. When the number and depth of trenches keep constant, the Bragg resonance peak value will increase at first and then decrease with the width of trenches, which implies that there exists a certain width of trenches to make the Bragg resonance peak value reach the maximum, laying a theoretical base for the optimization of Bragg resonance vs. the trench width. Particularly, the phase upshift of the Bragg resonance wave reflection peak value recently observed over finite periodically arranged cycloidal trenches, was confirmed again over the parabolic trenches. That implies that, the phase upshift of the Bragg resonance reflection peak value is a common phenomenon excited by finite periodic trenches with arbitrary cross sections. Consequently, for sinusoidal ripples and periodic artificial bars, the phase of the Bragg resonance reflection will shift downward, while for an array of periodic trenches, regardless of the shape of the trench cross section, the phase of the Bragg resonance reflection will shift upward. In addition, starting from the initial definition of the Bragg resonance, the mathematical mechanism of the phenomenon of phase upshift is well explained.
-
-
[1] BRAGG W H, BRAGG W L. The reflection of X-rays by crystal[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1913, 88(605): 428-438. [2] DAVIES A G. The reflection of wave energy by undulations on the seabed[J]. Dynamics of Atmospheres and Oceans, 1982, 6(4): 207-232. doi: 10.1016/0377-0265(82)90029-X [3] HEATHERSHAW A D. Seabed-wave resonance and sand bar growth[J]. Nature, 1982, 296(5855): 343-345. doi: 10.1038/296343a0 [4] DAVIES A G, HEATHERSHAW A D. Surface-wave propagation over sinusoidally varying topography[J]. Journal of Fluid Mechanics, 1984, 144(1): 419-443. [5] MEI C C. Resonant reflection of surface waters by periodic sandbars[J]. Journal of Fluid Mechanics, 1985, 152(1): 315-335. [6] DALRYMPLE R A, KIRBY J T. Water waves over ripples[J]. Journal of Waterway Port Coastal Ocean Engineering, 1986, 112(2): 309-319. doi: 10.1061/(ASCE)0733-950X(1986)112:2(309) [7] KIRBY J T. Current effects on resonant reflection of surface water waves by sand bars[J]. Journal of Fluid Mechanics, 1988, 186: 501-520. doi: 10.1017/S0022112088000242 [8] BELZONS M, REY V, GUAZZELLI E. Subharmonic Bragg resonance for surface water waves[J]. Europhysics Letters, 1991, 16: 189-194. [9] GUAZZELLI E, REY V, BELZONS M. Higher-order Bragg reflection of gravity surface water waves[J]. Journal of Fluid Mechanics, 1992, 245: 301-317. doi: 10.1017/S0022112092000478 [10] CHAMBERLAIN P G, PORTER D. The modified mild-slope equation[J]. Journal of Fluid Mechanics, 1995, 291: 393-407. doi: 10.1017/S0022112095002758 [11] LIU Y, YUE D K P. On generalized Bragg scattering of surface waves by bottom ripples[J]. Journal of Fluid Mechanics, 1998, 356(1): 297-326. [12] ARDHUIN F, HERBERS T H C. Bragg scattering of random surface gravity waves by irregular seabed topography[J]. Journal of Fluid Mechanics, 2002, 451(1): 1-33. [13] PORTER R, PORTER D. Scattered and free waves over periodic beds[J]. Journal of Fluid Mechanics, 2003, 483: 129-163. doi: 10.1017/S0022112003004208 [14] LIU H W, LI X F, LIN P. Analytical study of Bragg resonance by singly periodic sinusoidal ripples based on the modified mild-slope equation[J]. Coastal Engineering, 2019, 150: 121-134. doi: 10.1016/j.coastaleng.2019.04.015 [15] LIU W, LIU Y, ZHAO X. Numerical study of Bragg reflection of regular water waves over fringing reefs based on a boussinesq model[J]. Ocean Engineering, 2019, 190: 106415. doi: 10.1016/j.oceaneng.2019.106415 [16] PENG J, TAO A F, LIU Y M, et al. A laboratory study of class Ⅲ Bragg resonance of gravity surface waves by periodic beds[J]. Physics of Fluids, 2019, 31(6): 067110. doi: 10.1063/1.5083790 [17] 彭冀. 高阶非线性对波浪布拉格共振影响机制研究[D]. 博士学位论文. 南京: 河海大学, 2020.PENG Ji. Influence mechanism of higher order nonlinearity on gravity wave Bragg resonance[D]. PhD Thesis. Nanjing: Hohai University, 2020.(in Chinese) [18] LIANG B, GE H, ZHANG L, et al. Wave resonant scattering mechanism of sinusoidal seabed elucidated by Mathieu Instability theorem[J]. Ocean Engineering, 2020, 218(2): 108238. [19] GAO J, MA X, DONG G, et al. Investigation on the effects of Bragg reflection on harbor oscillations[J]. Coastal Engineering, 2021, 170: 103977. doi: 10.1016/j.coastaleng.2021.103977 [20] MEI C C, HARA T, NACIRI M. Note on Bragg scattering of water waves by parallel bars on the seabed[J]. Journal of Fluid Mechanics, 1988, 186: 147-162. doi: 10.1017/S0022112088000084 [21] HSU T W, TSAI L H, HUANG Y T. Bragg scattering of water wave by multiply composite artificial bars[J]. Coastal Engineering Journal, 2003, 45(2): 235-253. doi: 10.1142/S0578563403000750 [22] JEON C H, CHO Y S. Bragg reflection of sinusoidal waves due to trapezoidal submerged breakwaters[J]. Ocean Engineering, 2006, 33(14/15): 2067-2082. [23] WANG S K, HSU T W, TSAI L H, et al. An application of Miles theory to Bragg scattering of water waves by doubly composite artificial bars[J]. Ocean Engineering, 2006, 33(3/4): 331-349. [24] CHANG H K, LIOU J C. Long wave reflection from submerged trapezoidal breakwaters[J]. Ocean Engineering, 2007, 34(1): 185-191. doi: 10.1016/j.oceaneng.2005.11.017 [25] LIU H W, LUO H, ZENG H D. Optimal collocation of three kinds of artificial bars for Bragg resonant reflection by long waves[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 2015, 141(3): 1-17. [26] LIU H W, SHI Y P, CAO D Q. Optimization to parabolic bars for maximum Bragg resonant reflection of long waves[J]. Journal of Hydrodynamics, 2015, 27(3): 840-847. [27] 刘焕文. 沙坝及人工沙坝引起海洋表面波Bragg共振反射的研究进展[J]. 应用数学和力学, 2016, 37(5): 459-471. (LIU Huanwen. Advances in research on Bragg resonance of ocean surface waves by sandbars an artificial sandbars[J]. Applied Mathematics and Mechanics, 2016, 37(5): 459-471.(in Chinese) doi: 10.3879/j.issn.1000-0887.2016.05.002 [28] LIU Y, LI H J, ZHU L. Bragg reflection of water waves by multiple submerged semi-circular breakwater[J]. Applied Ocean Research, 2016, 56: 67-78. doi: 10.1016/j.apor.2016.01.008 [29] ZENG H, QIN B, ZHANG J. Optimal collocation of Bragg breakwaters with rectangular bars on sloping seabed for Bragg resonant reflection by long waves[J]. Ocean Engineering, 2017, 130: 156-165. doi: 10.1016/j.oceaneng.2016.11.066 [30] LIU H W, ZENG H D, HUANG H D. Bragg resonant reflection of surface waves from deep water to shallow water by a finite array of trapezoidal bars[J]. Applied Ocean Research, 2020, 94: 101976. doi: 10.1016/j.apor.2019.101976 [31] ZHANG H, TAO A, TU J, et al. The focusing waves induced by Bragg resonance with V-shaped undulating bottom[J]. Journal of Marine Science and Engineering, 2021, 9: 708. [32] HAO J, LI J, LIU S, et al. Wave amplification caused by Bragg resonance on parabolic-type topography[J]. Ocean Engineering, 2022, 244: 110442. [33] KAR P, KOLEY S, SAHOO T. Scattering of surface gravity waves over a pair of trenches[J]. Applied Mathematical Modelling, 2018, 62: 302-320. [34] KAR P, KOLEY S, SAHOO T. Bragg scattering of long waves by an array of trenches[J]. Ocean Engineering, 2020, 198: 107004. doi: 10.1016/j.oceaneng.2020.107004 [35] GUO F C, LIU H W, PAN J J. Phase downshift or upshift of Bragg resonance for water wave reflection by an array of cycloidal bars of trenches[J]. Wave Motion, 2021, 106: 102794. doi: 10.1016/j.wavemoti.2021.102794 [36] LIU H W, GUO F C, NI Y L. Analytical modeling of the wave reflection by a single cycloidal geotube or trench based on the modified mild-slope equation[J]. Journal of Engineering Mechanics, 2021, 148: 04021152. [37] LIU H W. Band gaps for Bloch waves over an infinite array of trapezoidal bars and triangular bars in shallow water[J]. Ocean Engineering, 2017, 130: 72-82. doi: 10.1016/j.oceaneng.2016.11.056 [38] LIU H W, LIU Y, LIN P. Bloch band gap of shallow-water waves over infinite arrays of parabolic bars and rectified cosinoidal bas and Bragg resonance over finite arrays of bars[J]. Ocean Engineering, 2019, 188: 106235. doi: 10.1016/j.oceaneng.2019.106235 [39] LIU H W, ZHOU X M. Explicit modified mild-slope equation for wave scattering by piecewise monotonic and piecewise smooth bathymetries[J]. Journal of Engineering Mathematics, 2014, 87(1): 29-45. doi: 10.1007/s10665-013-9661-6 [40] LIU H W, XIE J J. Series solution to the modified mild-slope equation for wave scatttering by Homma islands[J]. Wave Motion, 2013, 50(4): 869-884. doi: 10.1016/j.wavemoti.2013.02.012 [41] SPIEGEL M R. Applied Differential Equations[M]. Prentice-Hall, 1981. [42] PORTER D, STAZIKER D. Extensions of the mild-slope equation[J]. Journal of Fluid Mechanics, 1995, 300: 367-382. doi: 10.1017/S0022112095003727 [43] 滕斌, 候志莹. 变化地形上波浪传播模拟的二维BEM模型[C]//第十九届中国海洋(岸)工程学术讨论会论文集. 重庆, 2019: 379-384.TENG Bin, HOU Zhiying. Two dimensional BEM model for modelling of wave propagation over varying topographies[C]//Proceedings of the 19th China Ocean (Shore) Engineering Symposium. Chongqing, 2019: 379-384.(in Chinese) [44] XIE J J, LIU H W. Analytical study for linear wave transformation by a trapezoidal breakwater or channel[J]. Ocean Engineering, 2013, 64: 49-59. doi: 10.1016/j.oceaneng.2013.02.009 [45] KIRBY J T, ANTON JP. Bragg reflection of waves by artificial bars[C]//Proceedings of the 22nd International Conference of Coastal Engineering. New York, 1990, 815: 481-510. [46] MATTIOLI F. Resonant reflection of a series of submerged breakwaters[J]. Il Nuovo Cimento C, 1990, 13: 823-833. doi: 10.1007/BF02511999 [47] MILES J. Oblique surface-wave diffraction by a cylindrical obstacle[J]. Dynamics of Atmosphere and Ocean, 1981, 6(2): 121-123. doi: 10.1016/0377-0265(81)90019-1 [48] BENDER C J, DEAN R G. Wave transformation by two-dimensional bathymetric anomalies with sloped transitions[J]. Coastal Engineering, 2003, 50(1/2): 61-84. [49] LINTON C. Water waves over arrays of horizontal cylinders: band gaps and Bragg resonance[J]. Journal of Fluid Mechanics, 2011, 670: 504-526. doi: 10.1017/S0022112010005471 -




 下载:
下载:








 渝公网安备50010802005915号
渝公网安备50010802005915号