Effects of Cone Angles on Nonlinear Vibration Responses of Functionally Graded Shells
-
摘要:
研究了受外载荷下圆锥角对功能梯度壳的非线性振动的影响。首先,根据Voigt模型,在圆锥壳的厚度方向上建立功能梯度材料属性模型。然后,考虑一阶剪切变形理论和von Kármán非线性,利用Hamilton原理推导了功能梯度圆锥壳的非线性运动方程。之后,应用Galerkin法对运动方程进行离散化处理,再根据Volmir假设将方程简化为单自由度的非线性微分方程。最后,采用谐波平衡法和Runge-Kutta法对方程进行求解,分析了功能梯度圆锥壳的幅频响应特性曲线,讨论了不同材料分布函数以及陶瓷体积分数指数对圆锥壳幅频响应的影响,描述了不同锥角下圆锥壳的分岔图和不同激励幅值下圆锥壳的时间历程和相图,进一步通过Poincaré图反映了圆锥壳运动状态。结果表明:功能梯度圆锥壳呈现“渐硬”弹簧非线性特性;锥角增大,功能梯度圆锥壳混沌运动的现象被抑制,不易产生运动不稳定性;激励幅值增大,功能梯度圆锥壳运动呈现周期到多周期再到混沌的过程。
-
关键词:
- 非线性振动 /
- 分岔 /
- Poincaré截面图 /
- 功能梯度 /
- 圆锥壳
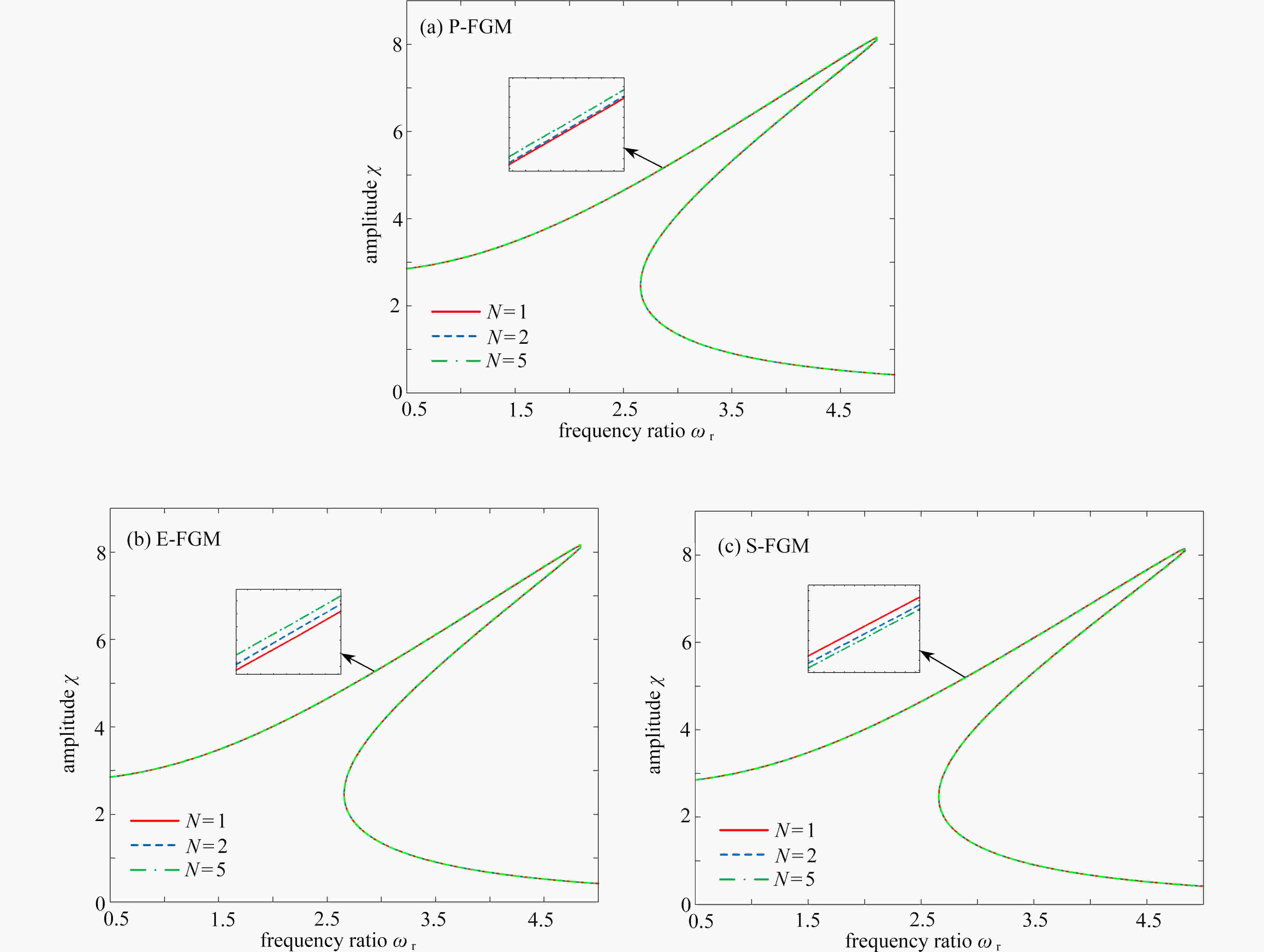
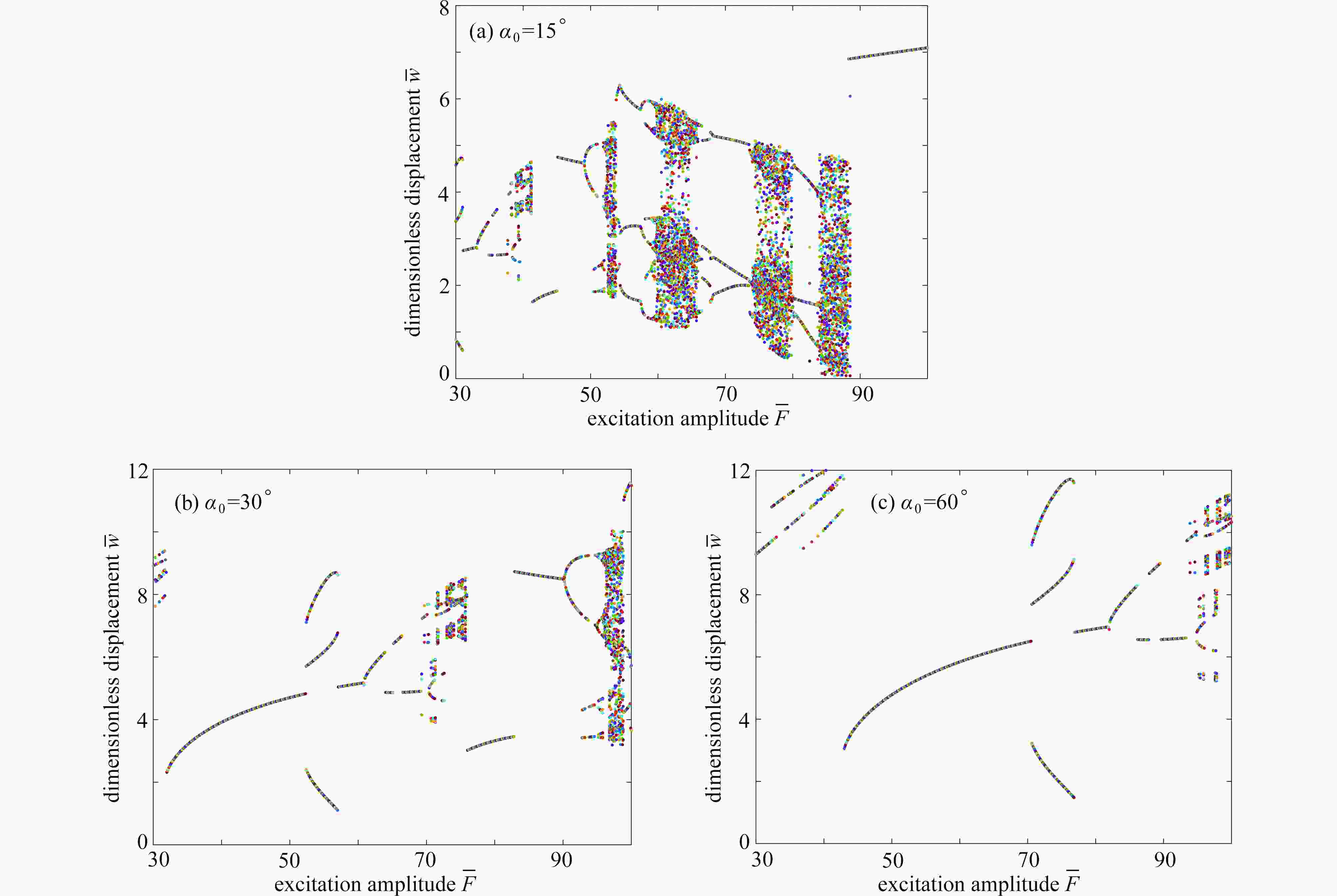
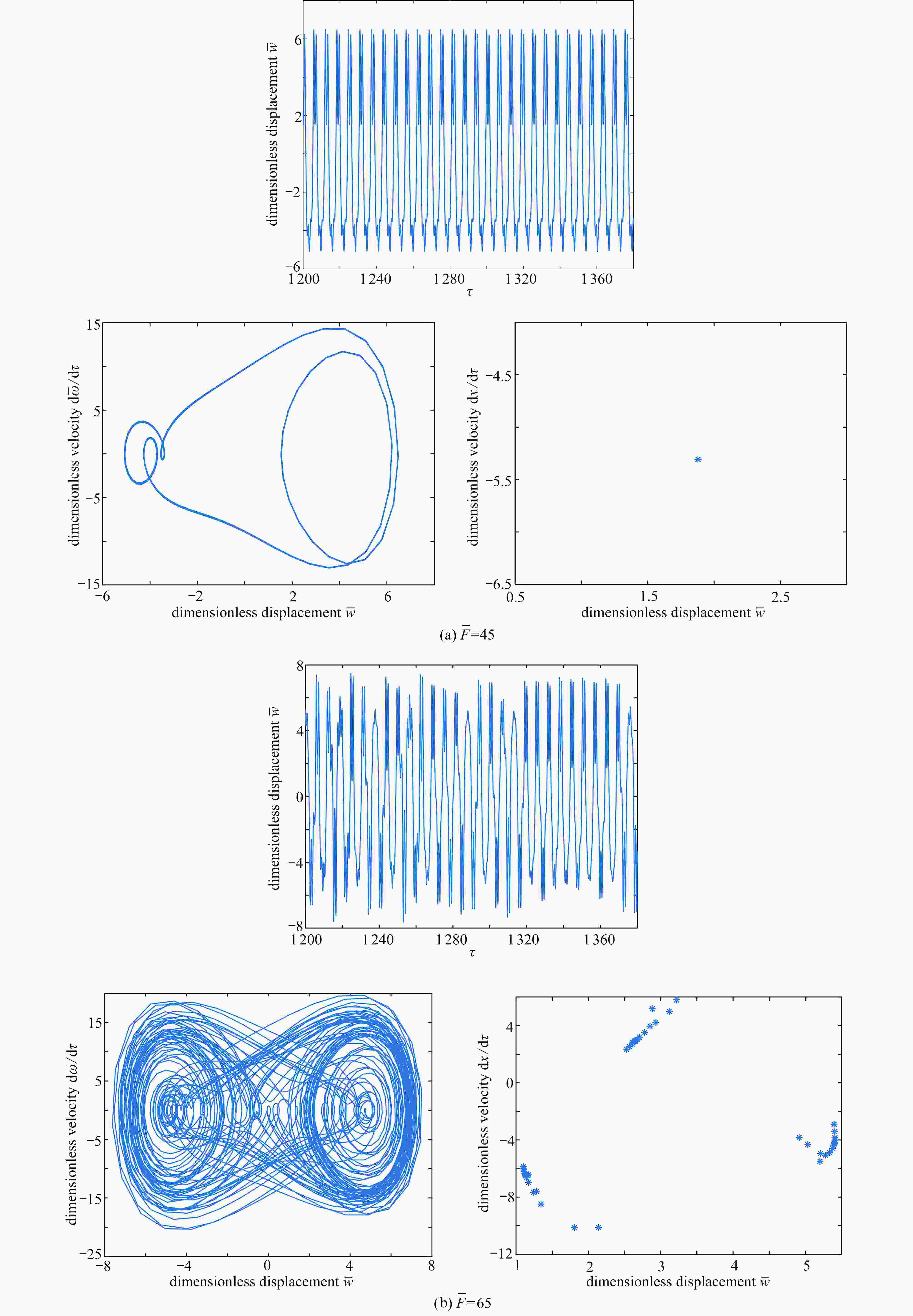
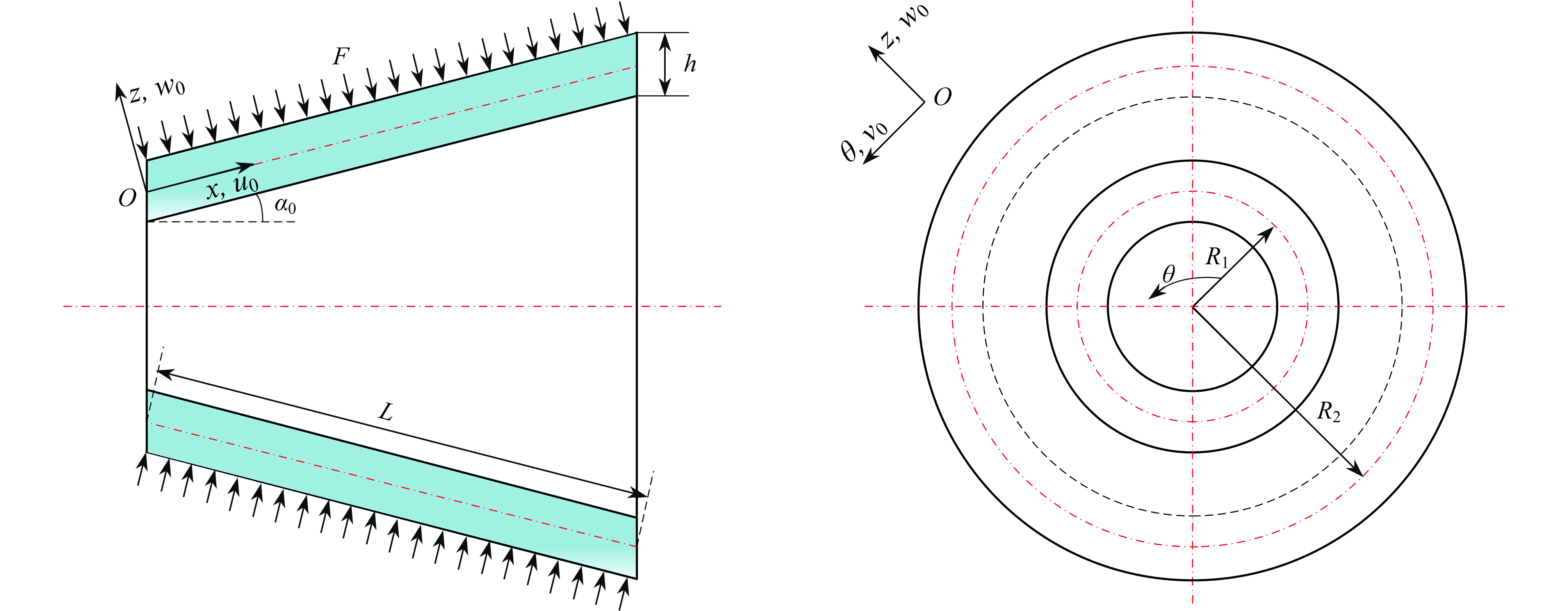
Abstract:The nonlinear vibration responses of functionally graded materials (FGMs) shells with different cone angles under external loads were studied. Firstly, the Voigt model was employed to describe the physical properties along the thickness direction of FGMs conical shells. Then, the motion equations were derived based on the 1st-order shear deformation theory, the von Kármán geometric nonlinearity and Hamilton’s principle. Next, the Galerkin method was applied to discretize the motion equations and the governing equations were simplified into a 1DOF nonlinear vibration differential equation under Volmir’s assumption. Finally, the nonlinear motion equations were solved with the harmonic balance method and the Runge-Kutta method, and the amplitude frequency response characteristic curves of the FGMs conical shells were obtained. The effects of different material distribution functions and different ceramic volume fraction exponents on the amplitude frequency response curves of conical shells were discussed. The bifurcation diagrams of conical shells with different cone angles, as well as time process diagrams and phase diagrams for different excitation amplitudes, were described. The motion characteristics were characterized by Poincaré maps. The results show that, the FGMs conical shells present the nonlinear characteristics of hardening springs. The chaotic motions of the FGMs conical shells are restrained and not prone to motion instability with the increase of the cone angle. The FGMs conical shell present a process from the periodic motion to the multi-periodic motion and then to chaos with the increase of the excitation amplitude.
-
Key words:
- nonlinear vibration /
- bifurcation /
- Poincaré map /
- functionally graded materials /
- conical shell
-
表 1 FGMs圆柱壳的材料参数
Table 1. Material parameters of FGMs cylindrical shells
material elastic module E/ GPa Poisson’s ratio ν density ρ/ (kg/m3) stainless steel 207.788 0.317 7 8 166 Ni 205.098 0.3 8 900 表 2 FGMs圆柱壳频率对比(R1=1, R1/h=500, L/R=20, m=1)
Table 2. Comparison of frequencies of FGMs cylindrical shells (R1=1, R1/h=500, L/R=20, m=1)
n f /HZ ref. [1] present 6 16.455 16.655 7 22.635 22.827 8 29.771 29.952 9 37.862 38.029 10 46.905 47.056 表 3 纯金属圆锥壳频率对比(R2=1, R2/h=100, Lsin(γ0)/R2=0.25, α0=30°, m=1)
Table 3. Comparison of frequencies of pure metal conical shells (R2=1, R2/h=100, Lsin(γ0)/R2=0.25, α0=30°, m=1)
-
[1] LOY C T, LAM K Y, REDDY J N. Vibration of functionally graded cylindrical shells[J]. International Journal of Mechanical Sciences, 1999, 41(3): 309-324. doi: 10.1016/S0020-7403(98)00054-X [2] 李世荣, 苏厚德, 程昌钧. 热环境中粘贴压电层功能梯度材料梁的自由振动[J]. 应用数学和力学, 2009, 30(8): 907-918 doi: 10.3879/j.issn.1000-0887.2009.08.003LI Shirong, SU Houde, CHENG Changjun. Free vibration of functionally graded material beams with surface-bonded piezoelectric layers in thermal environment[J]. Applied Mathematics and Mechanics, 2009, 30(8): 907-918.(in Chinese) doi: 10.3879/j.issn.1000-0887.2009.08.003 [3] 徐坤, 陈美霞, 谢坤. 正交各向异性功能梯度材料平板振动分析[J]. 噪声与振动控制, 2016, 36(4): 14-20XU Kun, CHEN Meixia, XIE Kun. Vibration analysis of orthotropic functionally graded plates[J]. Noise and Vibration Control, 2016, 36(4): 14-20.(in Chinese) [4] 李文达, 杜敬涛, 杨铁军, 等. 弹性边界约束旋转功能梯度圆柱壳结构自由振动行波特性分析[J]. 应用数学和力学, 2015, 36(7): 710-724 doi: 10.3879/j.issn.1000-0887.2015.07.004LI Wenda, DU Jingtao, YANG Tiejun, et al. Traveling wave mode characteristics of rotating functional gradient material cylindrical shell structures with elastic boundary constraints[J]. Applied Mathematics and Mechanics, 2015, 36(7): 710-724.(in Chinese) doi: 10.3879/j.issn.1000-0887.2015.07.004 [5] 田宏业, 刘朋, 胡志宽, 等. 基于半解析法的功能梯度圆锥板自由振动特性[J]. 船舶力学, 2021, 25(3): 351-359 doi: 10.3969/j.issn.1007-7294.2021.03.011TIAN Hongye, LIU Peng, HU Zhikuan, et al. Free vibration characteristics of functionally graded conical panels with complex boundary conditions[J]. Journal of Ship Mechanics, 2021, 25(3): 351-359.(in Chinese) doi: 10.3969/j.issn.1007-7294.2021.03.011 [6] LIANG X, ZHA X, YU Y, et al. Semi-analytical vibration analysis of FGM cylindrical shells surrounded by elastic foundations in a thermal environment[J]. Composite Structures, 2019, 223: 110997. doi: 10.1016/j.compstruct.2019.110997 [7] 杜长城, 李映辉, 金学松. 热环境中功能梯度圆柱壳内共振非线性模态[J]. 振动与冲击, 2014, 33(6): 161-164, 178DU Changcheng, LI Yinghui, JIN Xuesong. Nonlinear normal modes of functionally graded cylindrical shells with internal resonance in thermal environment[J]. Journal of Vibration and Shock, 2014, 33(6): 161-164, 178.(in Chinese) [8] LIU Y F, QIN Z Y, CHU F L. Nonlinear forced vibrations of FGM sandwich cylindrical shells with porosities on an elastic substrate[J]. Nonlinear Dynamics, 2021, 104(2): 1007-1021. doi: 10.1007/s11071-021-06358-7 [9] HAMID A, HABIB A. Nonlinear vibration analysis of FGM truncated conical shells subjected to harmonic excitation in thermal environment[J]. Mechanics Research Communications, 2020, 104(12): 103499. [10] SINGH S J, HARSHA S P. Nonlinear vibration analysis of sigmoid functionally graded sandwich plate with ceramic-FGM-metal layers[J]. Journal of Vibration Engineering & Technologies, 2020, 8(1): 67-84. [11] YANG S W, ZHANG W, HAO Y X, et al. Nonlinear vibrations of FGM truncated conical shell under aerodynamics and in-plane force along meridian near internal resonances[J]. Thin-Walled Structures, 2019, 142: 369-391. doi: 10.1016/j.tws.2019.04.024 [12] NGUYEN D D. Nonlinear thermo- electro-mechanical dynamic response of shear deformable piezoelectric sigmoid functionally graded sandwich circular cylindrical shells on elastic foundations[J]. Journal of Sandwich Structures & Materials, 2018, 20(3): 351-378. [13] MOGHADDAM S M F, AHMADI H. Active vibration control of truncated conical shell under harmonic excitation using piezoelectric actuator[J]. Thin-Walled Structures, 2020, 151: 106642. doi: 10.1016/j.tws.2020.106642 [14] 盛国刚. 压电与功能梯度圆柱壳的力学特性研究[D]. 博士学位论文. 上海: 上海交通大学, 2009.SHENG Guogang. Research on the property of mechanics of piezoelectric and functionally graded cylindrical shells[D]. PhD Thesis. Shanghai: Shanghai Jiao Tong University, 2009. (in Chinese) [15] ZHU C S, FANG X Q, LIU J X, et al. Smart control of large amplitude vibration of porous piezoelectric conical sandwich panels resting on nonlinear elastic foundation[J]. Composite Structures, 2020, 246: 112384. doi: 10.1016/j.compstruct.2020.112384 [16] NAJAFOV A M, SOFIYEV A H. The non-linear dynamics of FGM truncated conical shells surrounded by an elastic medium[J]. International Journal of Mechanical Sciences, 2013, 66: 33-44. doi: 10.1016/j.ijmecsci.2012.10.006 [17] LIEW K M, NG T Y, ZHAO X. Free vibration analysis of conical shells via the element-free kp-Ritz method[J]. Journal of Sound and Vibration, 2005, 281(3/5): 627-645. -





 下载:
下载:



 渝公网安备50010802005915号
渝公网安备50010802005915号