Secondary Buckling Analysis of Thin Rectangular Plates Based on the Wavelet Galerkin Method
-
摘要:
通过经典的弹性矩形薄板,研究了小波Galerkin法(WGM)在非线性屈曲问题数值求解方面的应用。首先,介绍了基于小波Galerkin法的von Kármán方程离散格式,然后提出了离散方程Jacobi矩阵和Hesse矩阵的一个简便计算方法,并讨论了基于小波离散格式的特征方程法、扩展方程法和伪弧长法等非线性屈曲分析方法。其次,较为详细地分析了弹性矩形薄板的二次屈曲平衡路径以及长宽比、边界条件和双向压缩对波形跳跃的影响。数值结果表明,小波Galerkin法在求解矩形板屈曲临界载荷时仍然有良好的收敛性,所获结果与稳定性实验、二次摄动法和非线性有限单元法的结果也非常一致,而结合不同分岔计算方法的可行性,更使其可为典型板壳的复杂非线性稳定性问题提供一种高效的空间离散方法。
-
关键词:
- 小波Galerkin法 /
- 矩形薄板 /
- 二次屈曲 /
- 波形跳跃
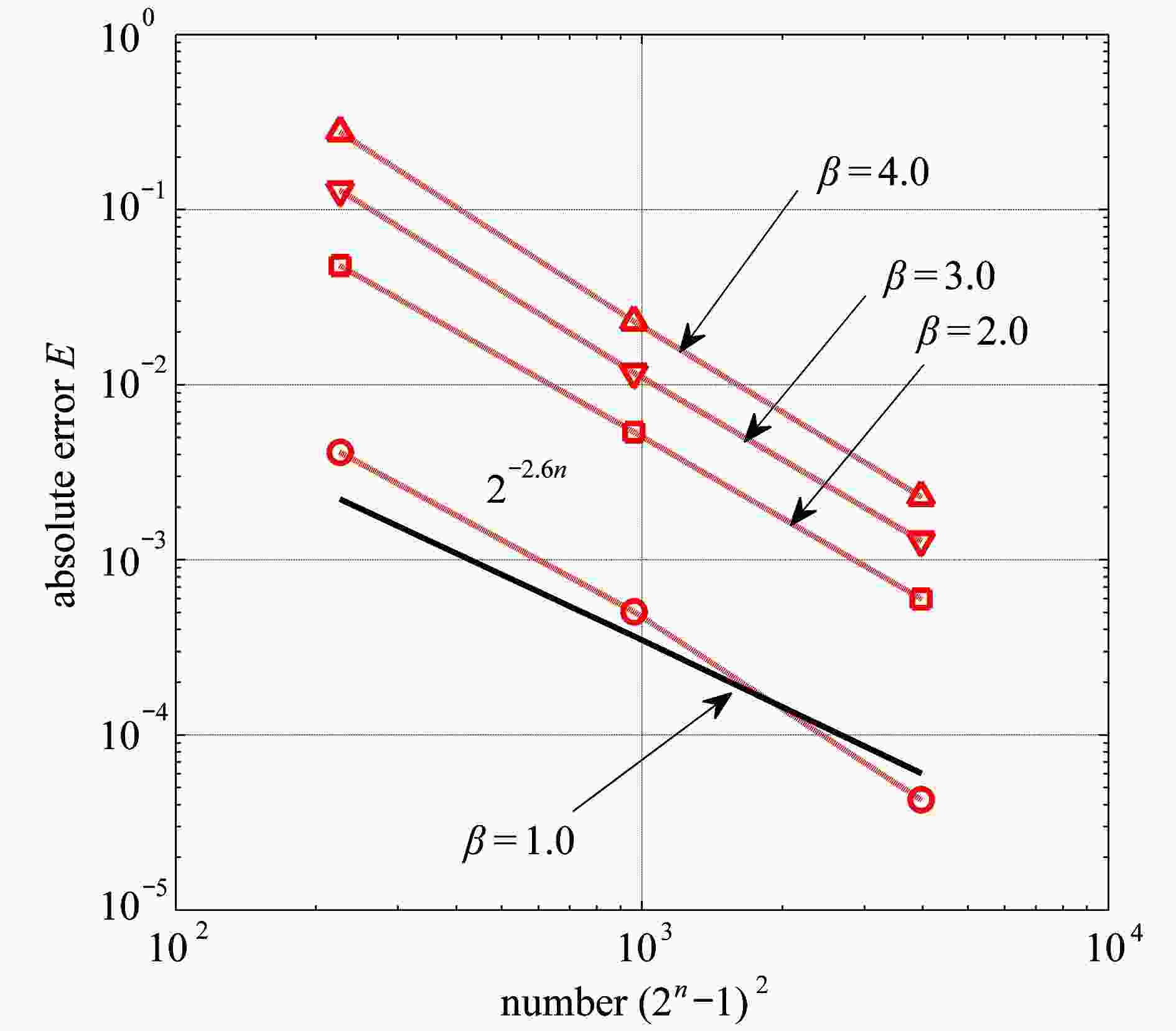
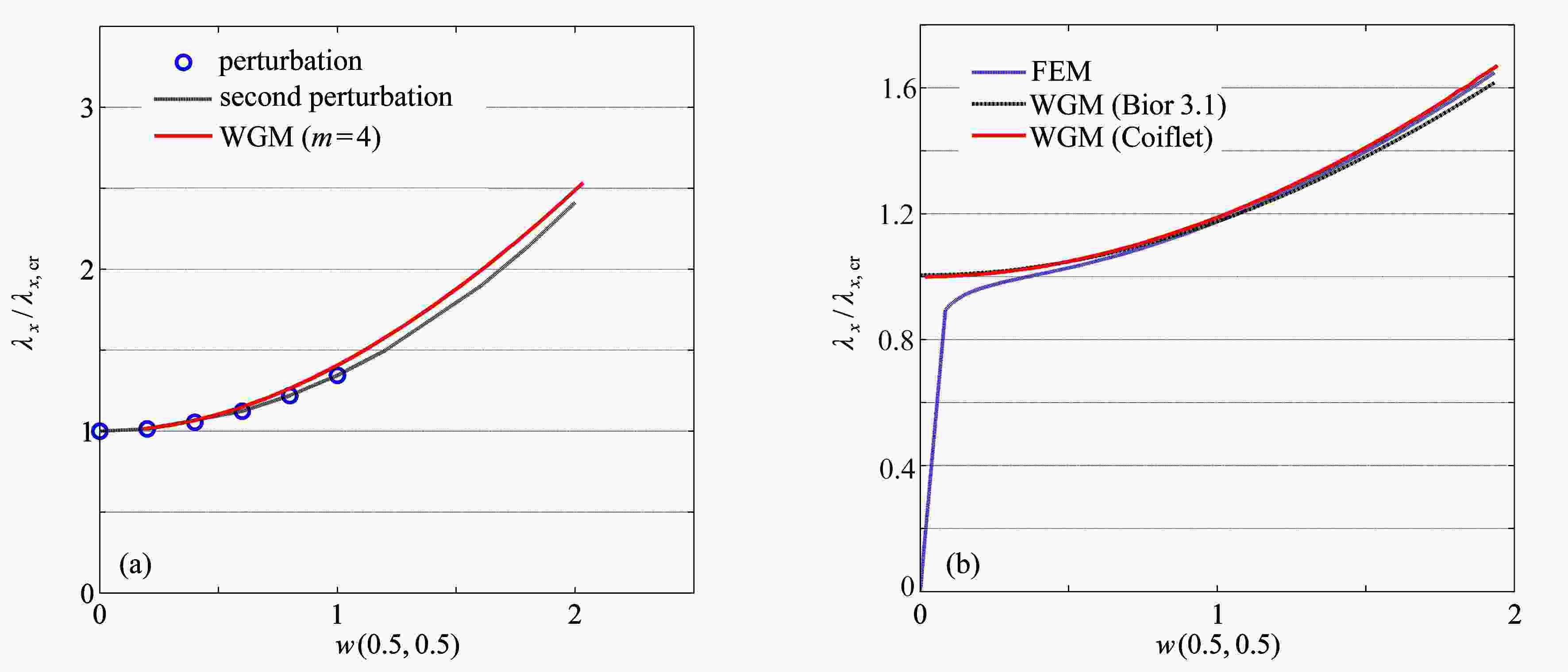
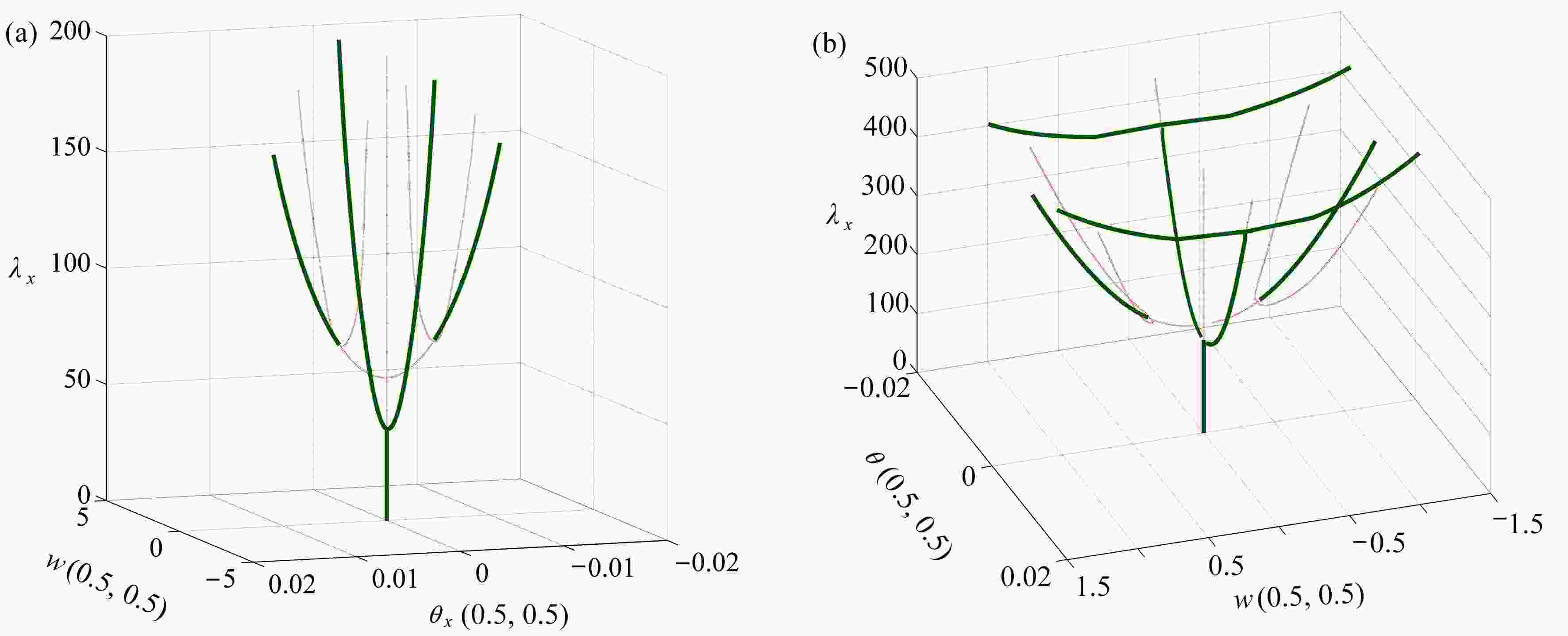
Abstract:Application of the wavelet Galerkin method (WGM) to numerical solution of nonlinear buckling problems was studied with classical elastic thin rectangular plates. First, the discretized scheme of the von Kármán equation were introduced, then a simple calculation approach to the Jacobian and Hessian matrices based on the WGM was proposed, and the wavelet discretized scheme-based eigenvalue equation method, the extended equation method and the pseudo arc-length method for nonlinear buckling analysis were discussed. Second, the secondary post-buckling equilibrium paths of elastic thin rectangular plates and the effects of aspect ratios, boundary conditions and bi-directional compression on the mode jumping behaviors, were discussed in detail. Numerical results show that, the WGM possesses good convergence for solving buckling loads on rectangular plates, and the obtained equilibrium paths are in good agreement with those from the stability experiments, the 2-step perturbation method and the nonlinear finite element method. Given the feasibility of combination with different bifurcation computation methods, the WGM makes an efficient spatial discretization method for complex nonlinear stability problems of typical plates and shells.
-
Key words:
- wavelet Galerkin method /
- rectangular thin plate /
- secondary buckling /
- mode jumping
-
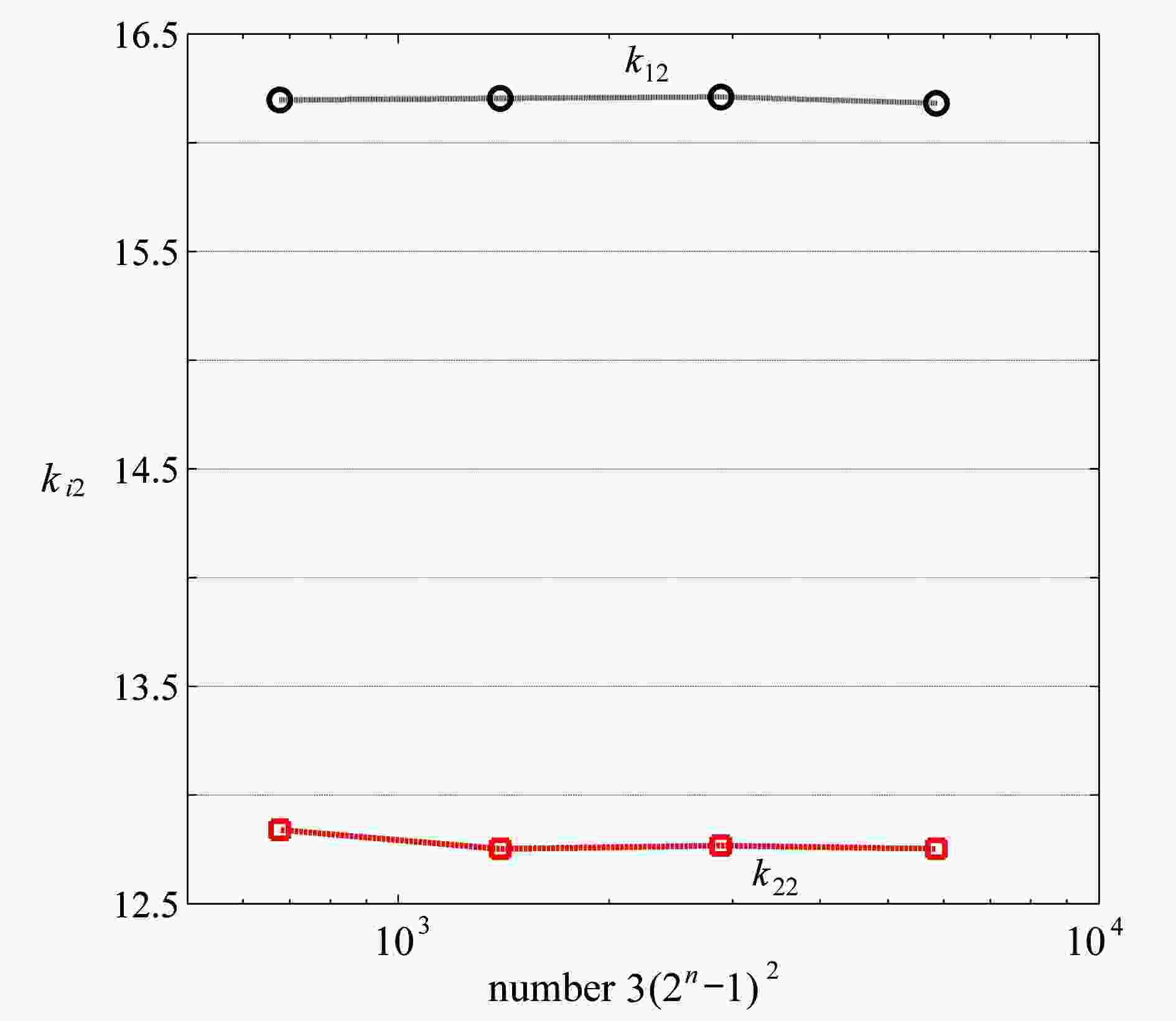
表 1 单向受压弹性矩形薄板的二次屈曲系数
Table 1. Secondary buckling coefficients of rectangular plates under uniaxial compression
β 4-edge simply supported 4-edge fixed k12 k22 k12 k22 1.0 174.518 7.715 16.210 12.767 1.5 21.693 5.292 24.259 13.066 2.0 11.139 5.351 45.893 13.297 2.5 57.023 4.302 10.315 8.099 3.0 55.059 4.694 52.947 9.087 -
[1] 刘小靖, 周又和, 王记增. 小波方法及其力学应用研究进展[J]. 应用数学和力学, 2022, 43(1): 1-13LIU Xiaojing, ZHOU Youhe, WANG Jizeng. Research progresses of wavelet methods and their applications in mechanics[J]. Applied Mathematics and Mechanics, 2022, 43(1): 1-13.(in Chinese) [2] ZHANG Lei, WANG Jizeng, ZHOU Youhe. Wavelet solution for large deflection bending problems of thin rectangular plate[J]. Archive of Applied Mechanics, 2015, 85: 355-365. doi: 10.1007/s00419-014-0960-9 [3] LIU X J, LIU G R, WANG J Z, et al. A wavelet multiresolution interpolation Galerkin method for targeted local solution enrichment[J]. Computational Mechanics, 2019, 64: 989-1016. doi: 10.1007/s00466-019-01691-6 [4] 杨骁, 程昌钧. 联合载荷作用下简支矩形板的屈曲和过屈曲[J]. 力学学报, 1992, 24(1): 82-92YANG Xiao, CHENG Changjun. The buckling and post-buckling of simply-supported rectangular plates under combination loads[J]. Acta Mechanica Sinica, 1992, 24(1): 82-92.(in Chinese) [5] 周祥玉, 范祖尧. 受压薄板后屈曲性态的试验研究[J]. 上海交通大学学报, 1992, 26(4): 14-19 doi: 10.16183/j.cnki.jsjtu.1992.04.003ZHOU Xiangyu, FAN Zuyao. An experiment study of post-buckling behavior of thin plates[J]. Journal of Shanghai Jiaotong University, 1992, 26(4): 14-19.(in Chinese) doi: 10.16183/j.cnki.jsjtu.1992.04.003 [6] JI Dongmei, CHEN Yanxia, HU Yuren. Application of the method of wavelet weighted residuals to post-buckling behavior of clamped rectangular plates[J]. Journal of Ship Mechanics, 2008, 12(3): 454-463. [7] 沈惠申. 板壳后屈曲行为[M]. 上海: 上海科学技术出版社, 2002.SHEN Huishen. Postbuckling Behaviors of Plates and Shells[M]. Shanghai: Shanghai Scientific & Technical Publishers, 2002. (in Chinese) [8] NAKAMURA T, UETANI K. The secondary buckling and post-secondary-buckling behaviors of rectangular plates[J]. International Journal of Mechanical Science, 1979, 21(5): 265-286. doi: 10.1016/0020-7403(79)90002-X [9] REZAIEE P M, MOGHADDASIE B. Stability boundaries of two-parameter non-linear elastic structures[J]. International Journal of Solids and Structures, 2014, 51(5): 1089-1102. doi: 10.1016/j.ijsolstr.2013.12.004 [10] 陈晓, 戴诗亮, 许可. 复合材料层合板的二次屈曲和二次分枝点分析[J]. 计算力学学报, 2002, 19(2): 42-47 doi: 10.3969/j.issn.1007-4708.2002.01.009CHEN Xiao, DAI Shiliang, XU Ke. Analysis of secondary buckling and secondary bifurcation point for composite laminated plates[J]. Chinese Journal of Computational Mechanics, 2002, 19(2): 42-47.(in Chinese) doi: 10.3969/j.issn.1007-4708.2002.01.009 [11] 吴柏生, 胡守信. 弹性基础上方形板的二次分叉[J]. 吉林大学自然科学学报, 1993, 4: 33-41WU Baisheng, HU Shouxin. Secondary bifurcation of a square plate on an elastic foundation[J]. Acta Scientiarum Naturalium Universitatis Jilinensis, 1993, 4: 33-41.(in Chinese) [12] 金明, 黄克服, 武际可. 方板弹性突跳的数值模拟, 第一部分: 理论和计算方案[J]. 工程力学, 2001, 18(5): 18-28 doi: 10.3969/j.issn.1000-4750.2001.05.003JIN Ming, HUANG Kefu, WU Jike. Numercial simulation of snap through of square plate, part Ⅰ: theory and numerical methods[J]. Engineering Mechanics, 2001, 18(5): 18-28.(in Chinese) doi: 10.3969/j.issn.1000-4750.2001.05.003 [13] 王记增. 正交小波统一理论与方法及其在压电智能结构等力学研究中的应用[D]. 博士学位论文. 兰州: 兰州大学, 2001.WANG Jizeng. Generalized theory and arithmetic of orthogonal wavelets and applications to researches of mechanics including piezoeiectric smart structures[D]. PhD Thesis. Lanzhou: Lanzhou University, 2001. (in Chinese) [14] 崔德刚. 结构稳定性设计手册[M]. 北京: 航空工业出版社, 1996.CUI Degang. Handbook of Structure Stability Design[M]. Beijing: Aviation Industry Press, 1996. (in Chinese) -




 下载:
下载:

 渝公网安备50010802005915号
渝公网安备50010802005915号