High Accuracy Numerical Simulation of Non-Isothermal Viscoelastic Polymer Fluid Past a Cylinder
-
摘要:
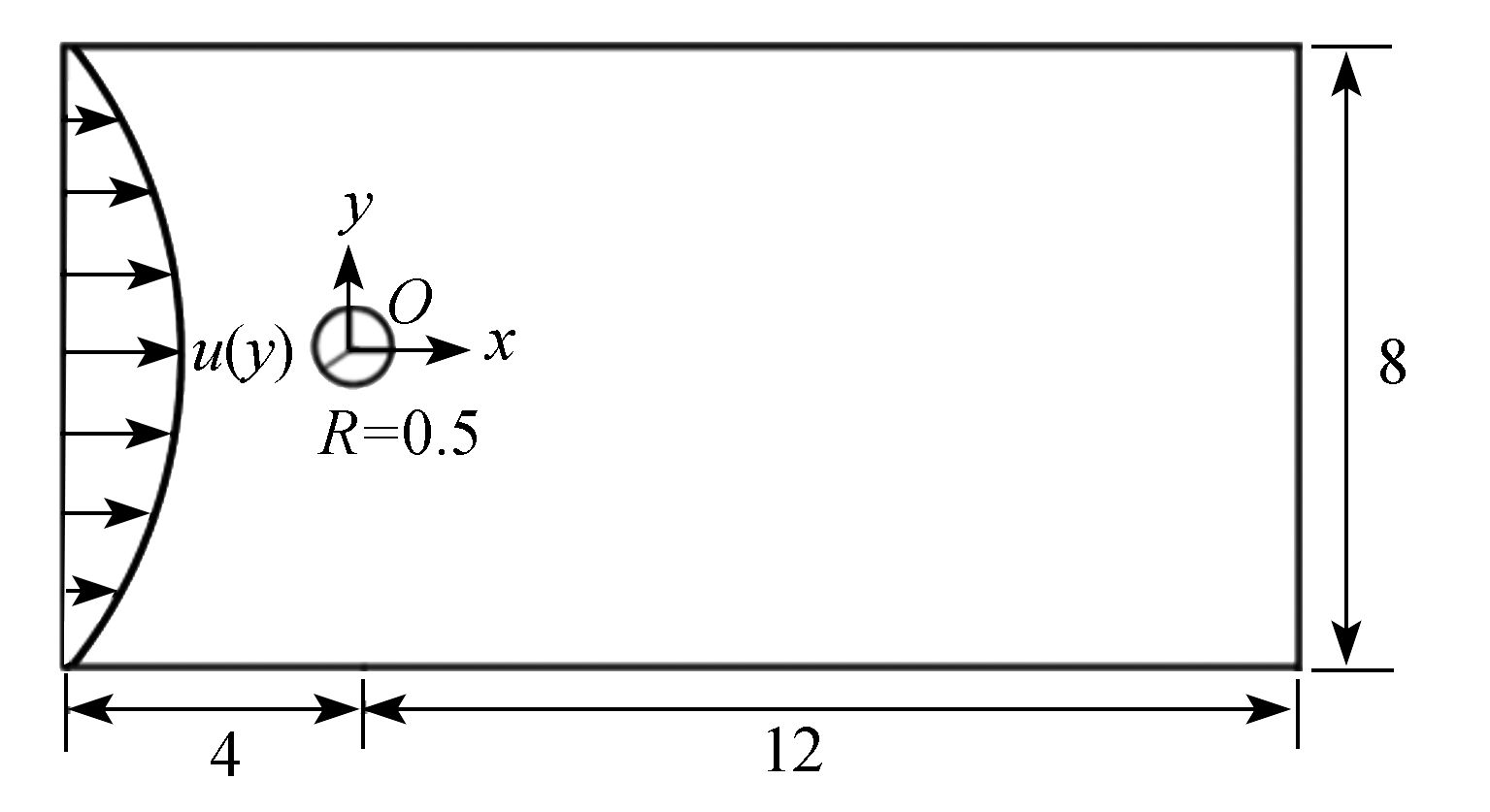
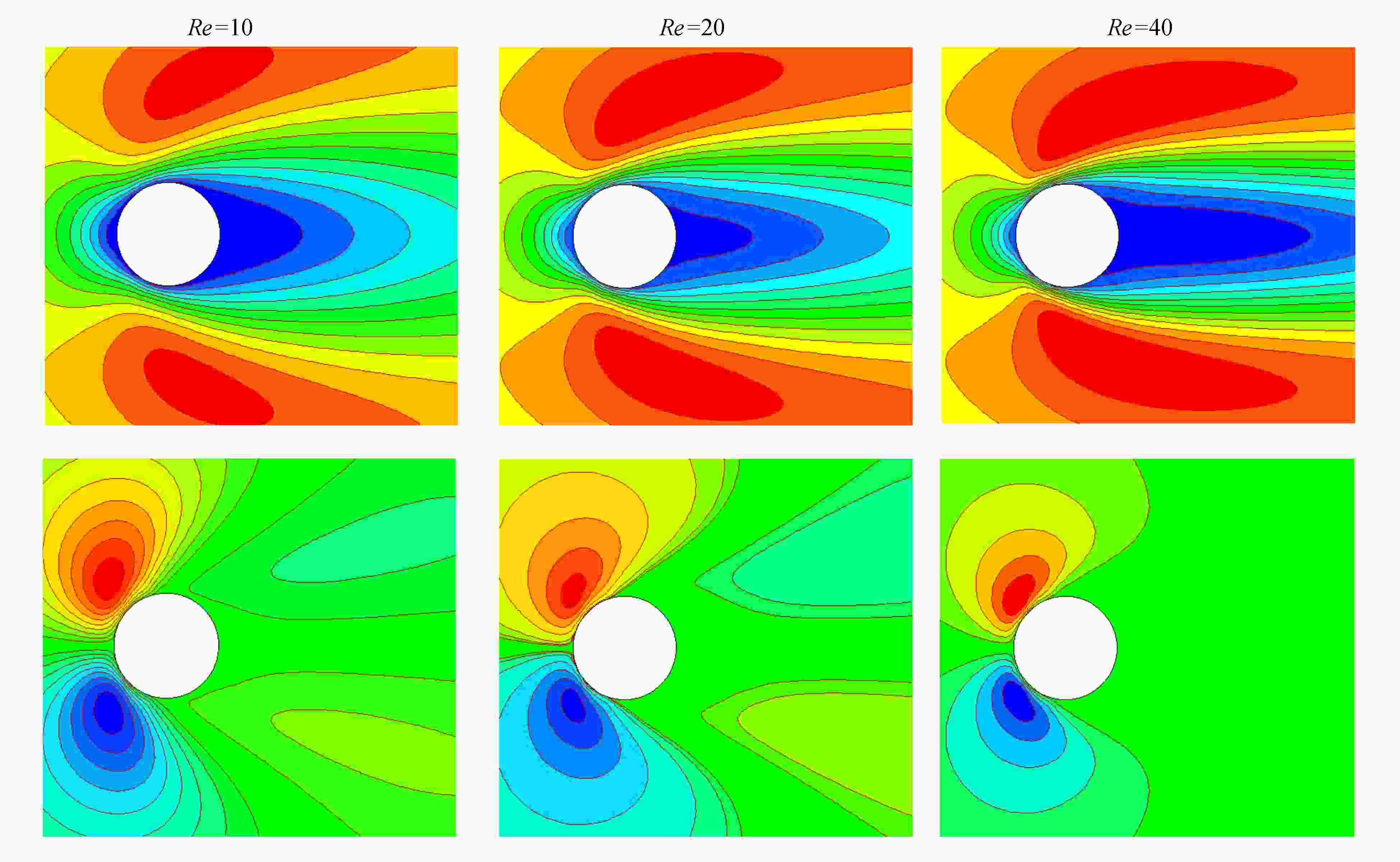
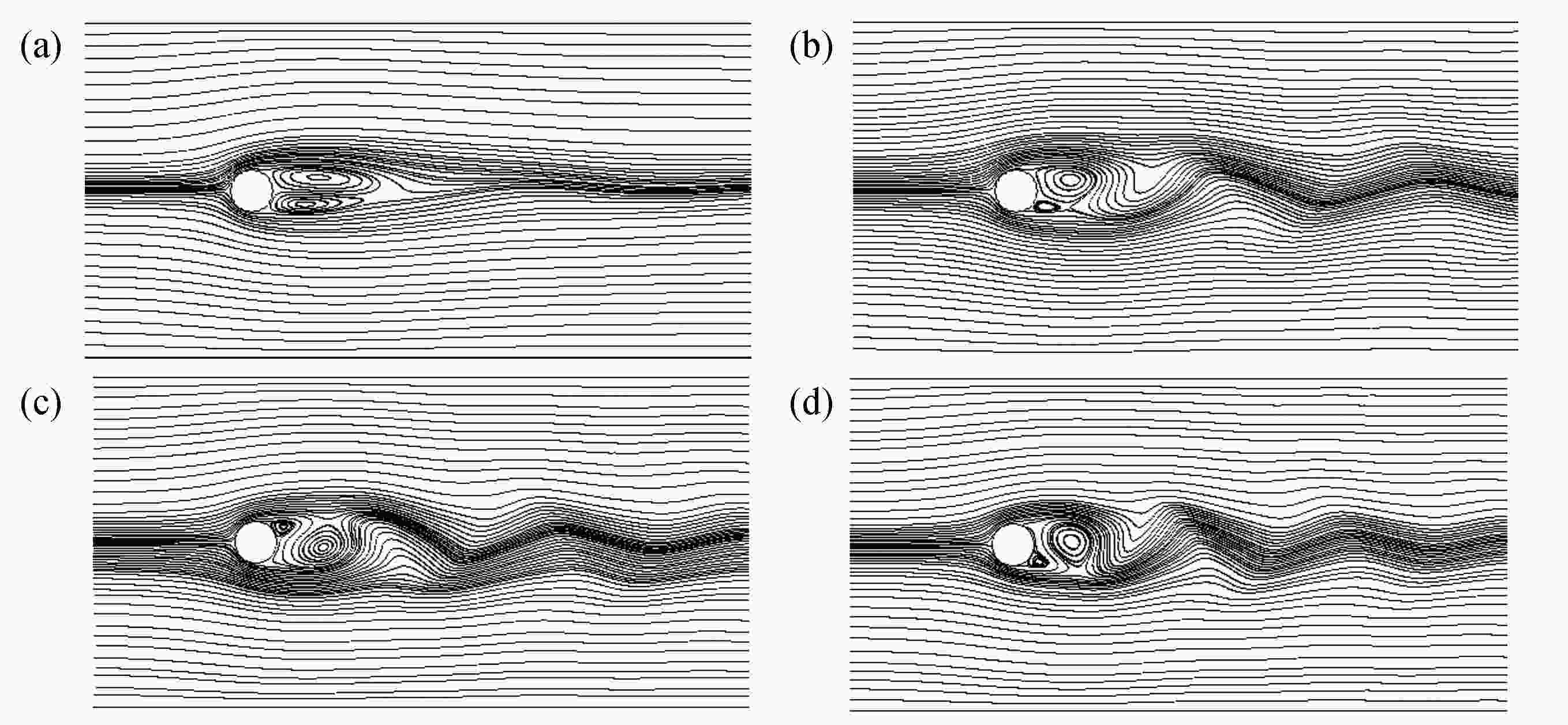
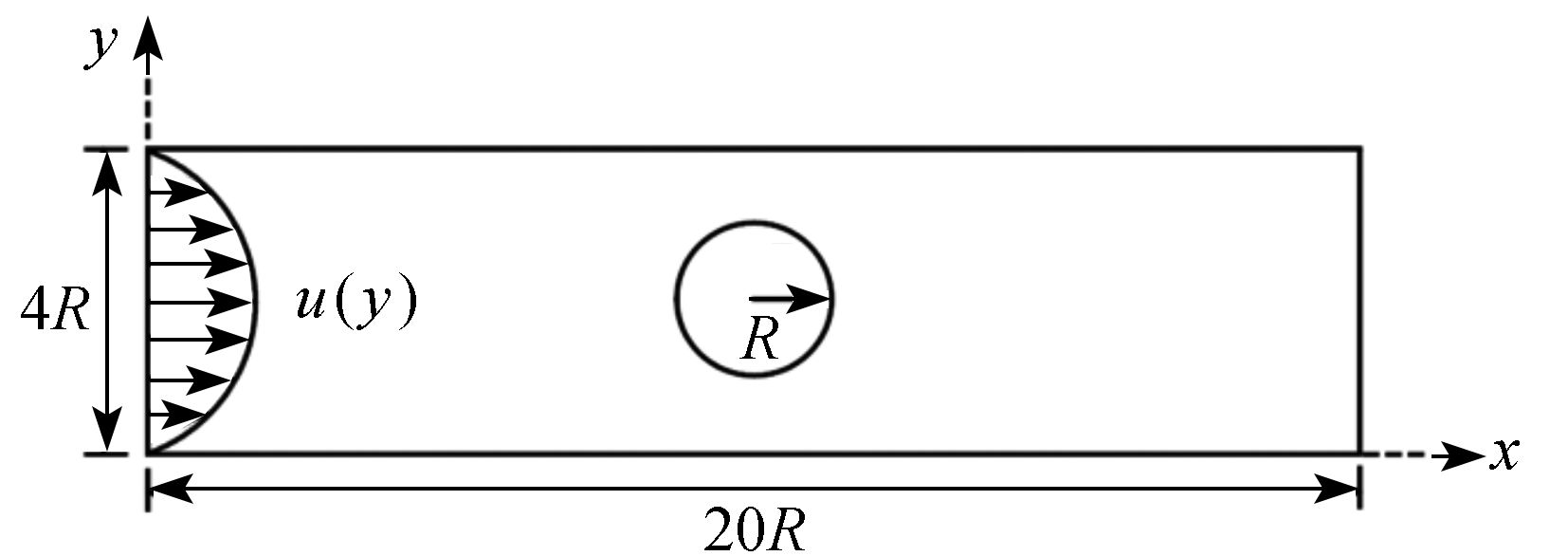
采用同位网格有限体积(coupled and linked equations algorithm revised,CLEAR)方法求解黏性和XPP (eXtended Pom-Pom)黏弹性流动的控制方程,基于延时修正方法构造了动量和本构方程对流项的高精度AVLsmart格式。首先,为了验证该文方法的有效性,对不同Reynolds数下不可压黏性流体圆柱绕流问题进行了模拟。随后,对等温及非等温不可压XPP黏弹性流体圆柱绕流问题进行了有效模拟,给出了速度矢量、应力分量、拉升量以及温度的分布规律,分析了We数对水平速度、法向应力及拉升量的影响。该文研究成果能为精确预测复杂型腔纤维增强黏弹性聚合物熔体动态充填过程提供理论基础。
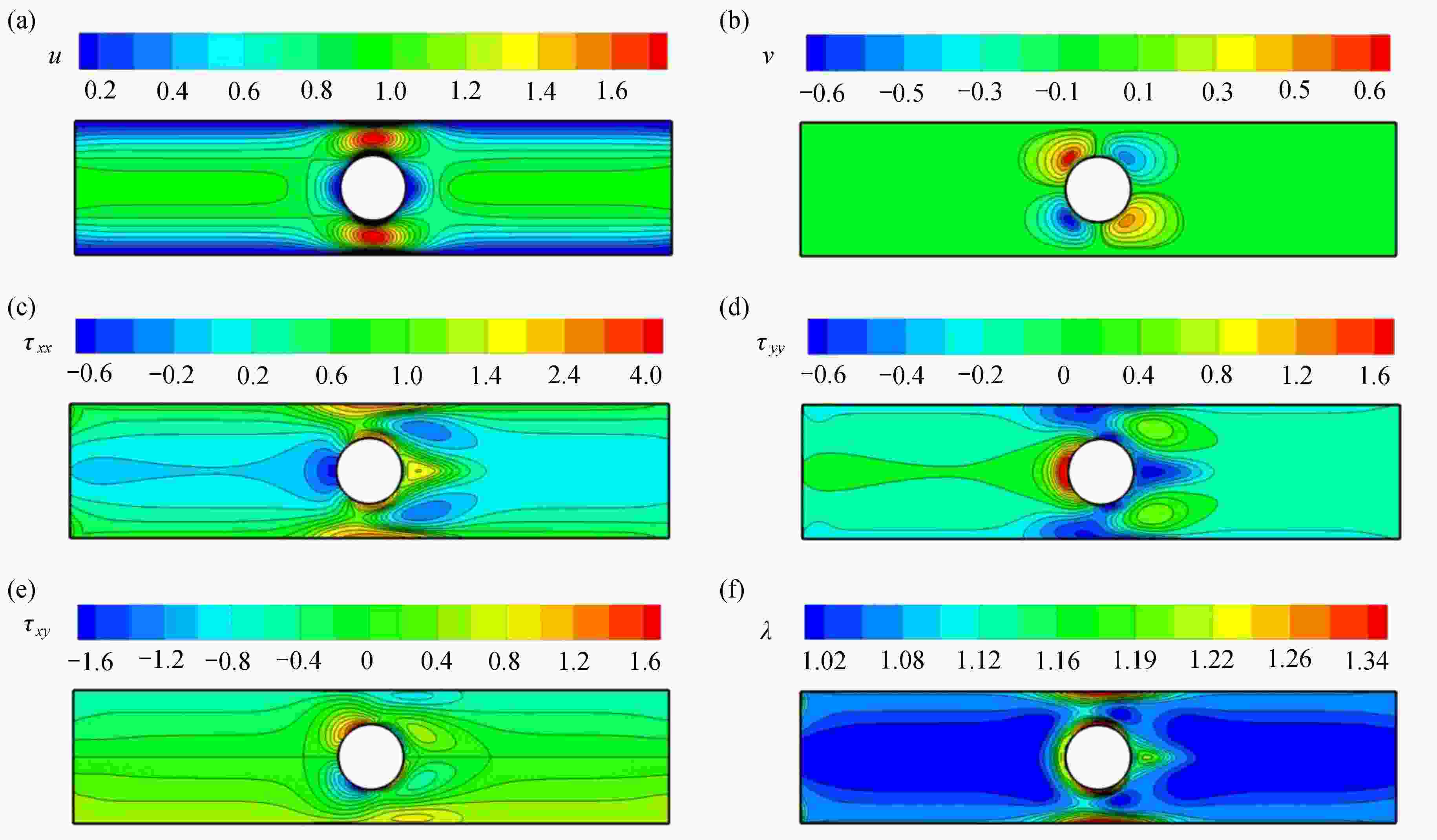
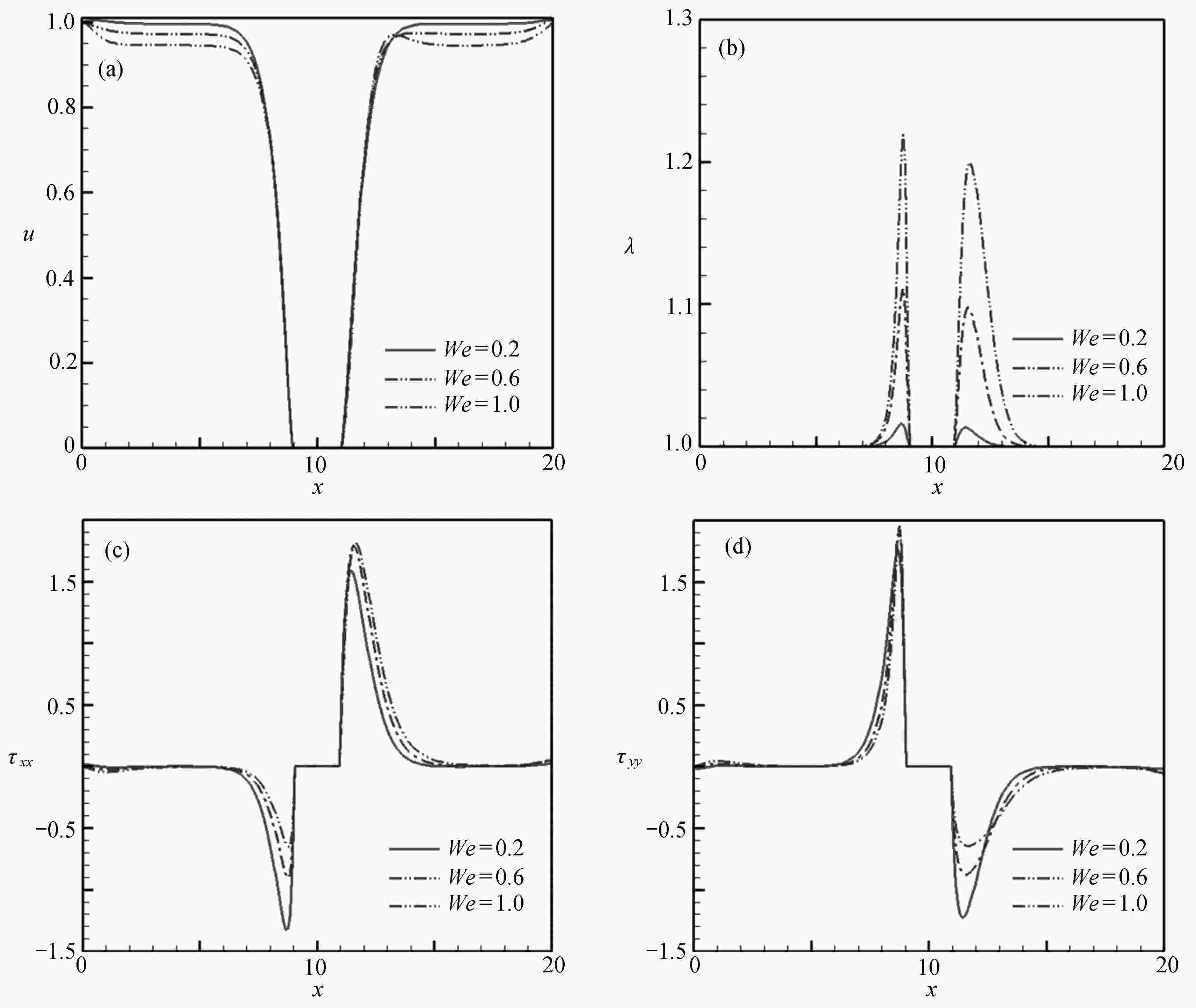
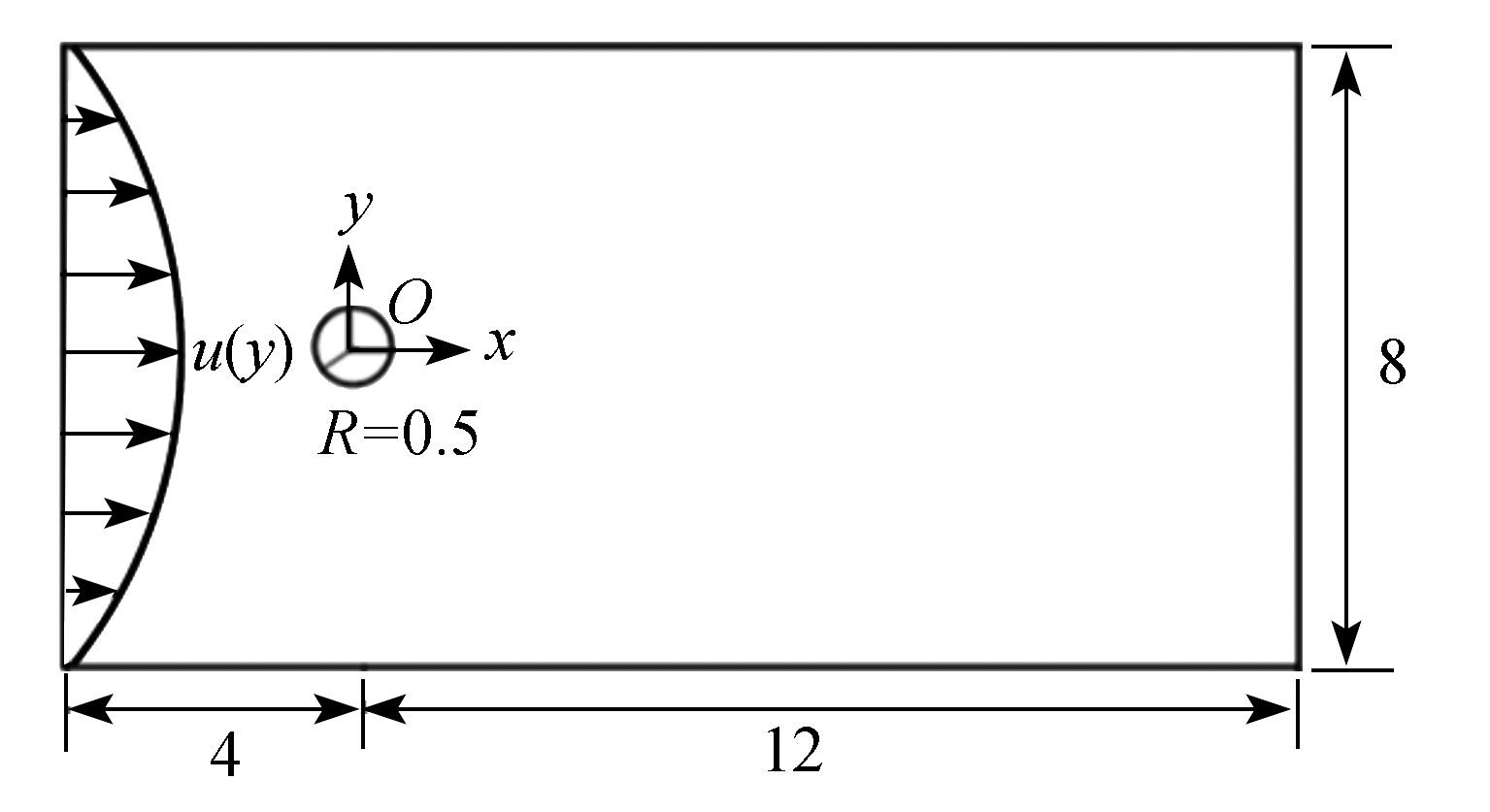
Abstract:The collocated grid finite volume CLEAR (coupled and linked equations algorithm revised) method was applied to solve the governing equations for viscous and XPP (eXtended Pom-Pom) viscoelastic fluids. The high accuracy AVLsmart schemes for the convection terms of momentum and constitutive equations were constructed based on the deferred correction method. Firstly, the incompressible viscous fluids past a cylinder at different Reynolds numbers were simulated to verify the validity of the developed numerical method. Then, the isothermal and non-isothermal XPP viscoelastic fluids past a cylinder were studied numerically, with the distribution patterns of velocity vectors, stress components, stretches and temperatures obtained. Especially, the effects of We on horizontal velocities, normal stresses and stretches were analyzed. The results provide a theoretical foundation for accurate prediction of fiber reinforced viscoelastic polymer dynamic filling process in complex cavities.
-
Key words:
- non-isothermal /
- XPP fluid /
- flow past a cylinder /
- high accuracy /
- numerical simulation
-
表 1 方程(18)中函数和常数的表达式
Table 1. Definition of functions and constants in eq. (18)
equation $ \varPhi $ $ \theta $ $ \delta $ $ {S_\varPhi } $ continuity 1 1 0 0 u-momentum $ u $ $ Re $ 1 $ - \dfrac{{\partial p}}{{\partial x}} + \left( {\dfrac{{\partial {\tau _{xx}}}}{{\partial x}} + \dfrac{{\partial {\tau _{xy}}}}{{\partial y}}} \right) + (\beta - 1)\left( {\dfrac{{{\partial ^2}u}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}u}}{{\partial {y^2}}}} \right) $ v-momentum $ v $ $ Re $ 1 $ - \dfrac{{\partial p}}{{\partial y}} + \left( {\dfrac{{\partial {\tau _{xy}}}}{{\partial x}} + \dfrac{{\partial {\tau _{yy}}}}{{\partial y}}} \right) + (\beta - 1)\left( {\dfrac{{{\partial ^2}v}}{{\partial {x^2}}} + \dfrac{{{\partial ^2}v}}{{\partial {y^2}}}} \right) $ $ {\tau _{xx}} $ normal stress $ {\tau _{xx}} $ $ We $ 0 $ {S_{{\tau _{xx}}}} $ $ {\tau _{xy}} $ shear stress $ {\tau _{xy}} $ $ We $ 0 $ {S_{{\tau _{xy}}}} $ $ {\tau _{yy}} $ normal stress $ {\tau _{yy}} $ $ We $ 0 $ {S_{{\tau _{yy}}}} $ energy $ T $ $ Pe $ 1 ${S_{{T} } }$ 表 2 不同Re下的曳力系数
Table 2. Drag coefficients at different Re numbers
表 3 LDPE熔体在
$ {T_{\text{r}}}{\text{ = 443}} $ 时的XPP和Arrhenius流变参数[9]Table 3. Rheology parameters for LDPE melt for the XPP and Arrhenius models at
$ {T_{\text{r}}}{\text{ = 443}} $ [9]parameters ${\lambda _{ {\text{0b} } } }({T_{\text{r} } })/{\rm{s }}$ $\lambda {}_{ {\text{0s} } }({T_{\text{r} } })/{\rm{s}}$ $ q $ $ \alpha $ ${\eta _{\text{s} } }/({\rm{Pa \cdot s}})$ ${\eta _0}/({\rm{Pa \cdot s} })$ $ {E_0}/({\text{J}} \cdot {\text{mo}}{{\text{l}}^{ - 1}}) $ $ R{\kern 1pt} /({\text{J}} \cdot {\text{mo}}{{\text{l}}^{ - 1}} \cdot {{\text{K}}^{ - 1}}{\text{)}} $ value 1.741 5 0.580 5 2 0.15 200 4 600 48 200 8.314 -
[1] 杨旭, 梁英杰, 孙洪广, 等. 空间分数阶非Newton流体本构及圆管流动规律研究[J]. 应用数学和力学, 2018, 39(11): 1213-1226YANG Xu, LIANG Yingjie, SUN Hongguang, et al. A study on the constitutive relation and the flow of spatial fractional non-Newtonian fluid in circular pipes[J]. Applied Mathematics and Mechanics, 2018, 39(11): 1213-1226.(in Chinese) [2] 吴其晔, 巫静安. 高分子材料流变学[M]. 北京: 高等教育出版社, 2002.WU Qiye, WU Jing’an. Polymer Rheology[M]. Beijing: Higher Education Press, 2002. (in Chinese) [3] 白羽, 方慧灵, 张艳. Oldroyd-B流体绕拉伸楔形体的非稳态滑移流动与传热分析[J]. 应用数学和力学, 2022, 43(3): 272-280BAI Yu, FANG Huiling, ZHANG Yan. Unsteady slip flow and heat transfer analysis of Oldroyd-B fluid over the stretching wedge[J]. Applied Mathematics and Mechanics, 2022, 43(3): 272-280.(in Chinese) [4] LIELENS G, KEUNINGS R, LEGAT V. The FENE-L and FENE-LS closure approximations to the kinetic theory of finitely extensible dumbbells[J]. Journal of Non-Newtonian Fluid Mechanics, 1999, 87(2/3): 179-196. [5] HYON Y K, DU Q, LIU C. An enhanced macroscopic closure approximation to the micro-macro FENE models for polymeric materials[J]. Multiscale Modeling Simulation, 2008, 7(2): 978-1002. doi: 10.1137/070708287 [6] PHAN-THIEN N, TANNER R I. A new constitutive equation derived from network theory[J]. Journal of Non-Newtonian Fluid Mechanics, 1977, 2(4): 353-365. doi: 10.1016/0377-0257(77)80021-9 [7] MCLEISH T C B, LARSON R G. Molecular constitutive equations for a class of branched polymers: the Pom-Pom polymer[J]. Journal of Rheology, 1998, 42(1): 81-110. doi: 10.1122/1.550933 [8] VERBEETEN W M H, PETERS G W M, BAAIJENS F T P. Differential constitutive equations for polymer melts: the extended Pom-Pom model[J]. Journal of Rheology, 2001, 45(4): 823-843. doi: 10.1122/1.1380426 [9] VERBEETEN W M H, PETERS G W M, BAAIJENS F P T. Viscoelastic analysis of complex polymer melt flows using the eXtended Pom-Pom model[J]. Journal of Non-Newtonian Fluid Mechanics, 2002, 108(1/3): 301-326. [10] VERBEETEN W M H, PETERS G W M, BAAIJENS F P T. Numerical simulations of the planar contraction flow for a polyethylene melt using the XPP model[J]. Journal of Non-Newtonian Fluid Mechanics, 2004, 117(2/3): 73-84. [11] TAMADDON-JAHROMI H R, WEBSTER M F. Transient behaviour of branched polymer melts through planar abrupt and rounded contractions using Pom-Pom models[J]. Mechanics of Time-Dependent Materials, 2011, 15: 181-211. doi: 10.1007/s11043-010-9130-9 [12] AGUAYOJP, PHILLIPSPM, PHILLIPSTN, et al. Thenumerical prediction of planar viscoelastic flows using the Pom-Pom model and high-order finite volumeschemes[J]. Journal of Computational Physics, 2007, 220(2): 586-611. doi: 10.1016/j.jcp.2006.05.039 [13] YANG B X, OUYANG J, LI Q, et al. Modeling and simulation of the viscoelastic fluid mold filling process by level set method[J]. Journal of Non-Newtonian Fluid Mechanics, 2010, 165(19/20): 1275-1293. [14] LI X J, HE J H. Variational multi-scale finite element method for the two-phase flow of polymer melt filling process[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2020, 30(3): 1407-1426. [15] OISHI C M, MARTINS F P, TOME M F, et al. Numerical solution of the eXtended Pom-Pom model for viscoelastic free surface flows[J]. Journal of Non-Newtonian Fluid Mechanics, 2011, 166(3/4): 165-179. [16] 曹伟, 王蕊, 申长雨. 塑料熔体在注塑模中的三维流动模拟[J]. 化工学报, 2004, 55(9): 1493-1498 doi: 10.3321/j.issn:0438-1157.2004.09.028CAO Wei, WANG Rui, SHEN Changyu. Three dimensional flow simulation of plastic melt in injection mold[J]. CIESC Journal, 2004, 55(9): 1493-1498.(in Chinese) doi: 10.3321/j.issn:0438-1157.2004.09.028 [17] 周文, 欧阳洁, 杨斌鑫, 等. 三维非等温非牛顿流体充模过程的建模与模拟[J]. 化工学报, 2011, 62(3): 618-627ZHOU Wen, OUYANG Jie, YANG Binxin, et al. Modeling and simulation of 3D non-isothermal non-Newtonian fluid filling process[J]. CIESC Journal, 2011, 62(3): 618-627.(in Chinese) [18] GAO P Y, ZHAO Z T, YANG Y. The numerical modeling and study of gas entrapment phenomenon in non-isothermal polymer filling process[J]. Journal of Non-Newtonian Fluid Mechanics, 2021, 294: 104575. doi: 10.1016/j.jnnfm.2021.104575 [19] CROCHET M J, PILATE G. Plane flow of a fluid of second grade through a contraction[J]. Journal of Non-Newtonian Fluid Mechanics, 1976, 1(3): 247-258. doi: 10.1016/0377-0257(76)80023-7 [20] PERERA M G N, WALTERS K. Long-range memory effects in flows involving abrupt changes in geometry, part Ⅰ: flows associated with L-shaped and T-shaped geometries[J]. Journal of Non-Newtonian Fluid Mechanics, 1977, 2(1): 49-81. doi: 10.1016/0377-0257(77)80032-3 [21] 陶文铨. 数值传热学[M]. 2版. 西安: 西安交通大学出版社, 2001.TAO Wenquan. Numerical Heat Transfer[M]. 2nd ed. Xi’an: Xi’an Jiaotong University Press, 2001.(in Chinese) [22] HABLA F, TAN M W, HABLBERGER J, et al. Numerical simulation of the viscoelastic flow in a three-dimensional lid-driven cavity using the log-conformation reformulation in OpenFOAM[J]. Journal of Non-Newtonian Fluid Mechanics, 2014, 212: 47-62. doi: 10.1016/j.jnnfm.2014.08.005 [23] PIMENTA F, ALVES M A. Stabilization of an open-source finite-volume solver for viscoelastic fluid flows[J]. Journal of Non-Newtonian Fluid Mechanics, 2017, 239: 85-104. doi: 10.1016/j.jnnfm.2016.12.002 [24] ZHOU W, OUYANG J, WANG X D, et al. Numerical simulation of viscoelastic fluid flows using a robust FVM framework on triangular grid[J]. Journal of Non-Newtonian Fluid Mechanics, 2016, 236: 18-34. doi: 10.1016/j.jnnfm.2016.08.003 [25] ZHUANG X, OUYANG J, LI Y G, et al. A three-dimensional thermal model for viscoelastic polymer melt packing process in injection molding[J]. Applied Thermal Engineering, 2018, 128: 1391-1403. doi: 10.1016/j.applthermaleng.2017.09.124 [26] TAO W Q, QU Z G, HE Y L. A novel segregated algorithm for incompressible fluid flow and heat transfer problems-CLEAR (coupled and linked equations algorithm revised) part Ⅰ: mathematical formulation and solution procedure[J]. Numerical Heat Transfer (Part B) : Fundamentals, 2004, 45(1): 1-17. [27] GAO P Y, OUYANG J, DAI P F, et al. A coupled continuous and discontinuous finite element method for the incompressible flows[J]. International Journal for Numerical Methods in Fluids, 2017, 84(8): 477-493. doi: 10.1002/fld.4358 [28] DING H, SHU C, YEO K S, et al. Simulation of incompressible viscous flow past a circular cylinder by hybrid FD scheme and meshless least squarebased finite difference method[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(9/11): 727-744. [29] NITHIARASU P, ZIENKIEWICZ O C. Analysis of an explicit and matrix free fractional stepmethod for incompressible flows[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(41/43): 5537-5551. [30] TUANN S Y, OLSON M D. Numerical studies of the flow around a circular cylinder by a finite element method[J]. Computers and Fluids, 1978, 6(4): 219-240. doi: 10.1016/0045-7930(78)90015-4 [31] 仇轶, 由长福, 祁海鹰, 等. 用无网格法求解不同Re下圆柱绕流问题[J]. 清华大学学报(自然科学版), 2005, 45(2): 220-223 doi: 10.3321/j.issn:1000-0054.2005.02.021QIU Yi, YOU Changfu, QI Haiying, et al. Numerical simulation of flow around a cylinder for different Re using a meshless method[J]. Journal Tsinghua University (Science and Technology) , 2005, 45(2): 220-223.(in Chinese) doi: 10.3321/j.issn:1000-0054.2005.02.021 -




 下载:
下载:






 渝公网安备50010802005915号
渝公网安备50010802005915号