The Panel Method for Rigid Section Group Added Mass Coefficients and Its Application to Fuel Assemblies
-
摘要:
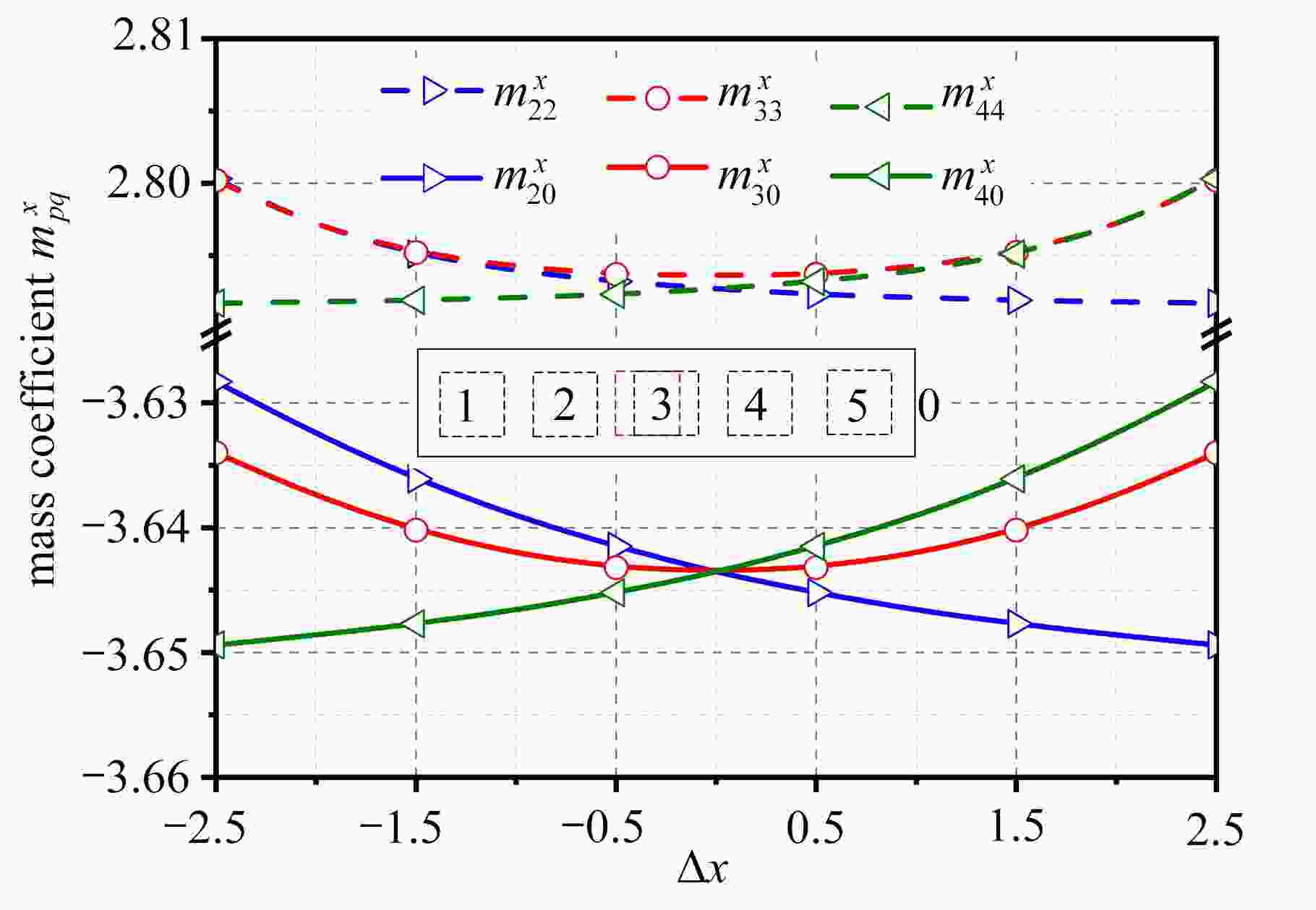
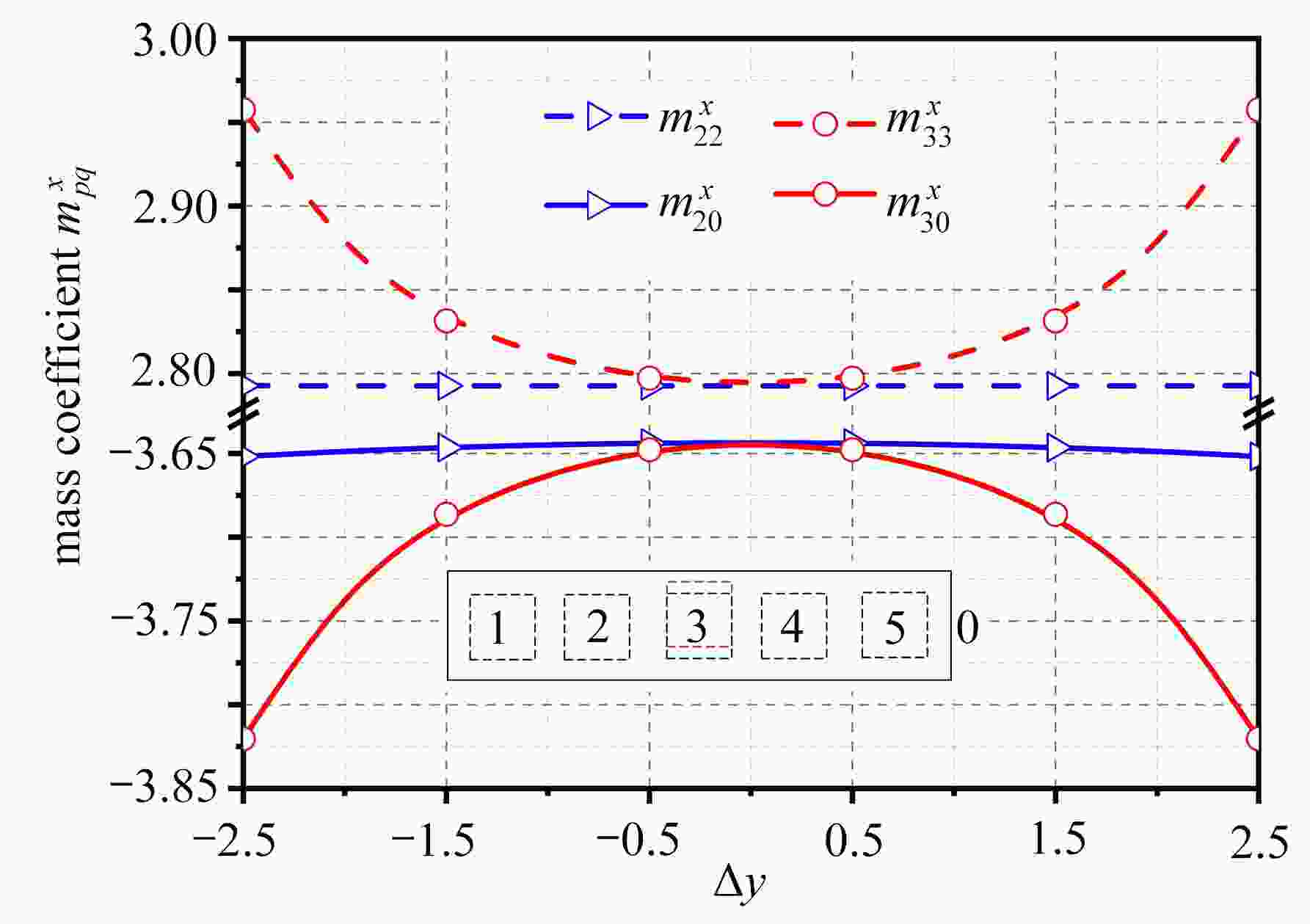
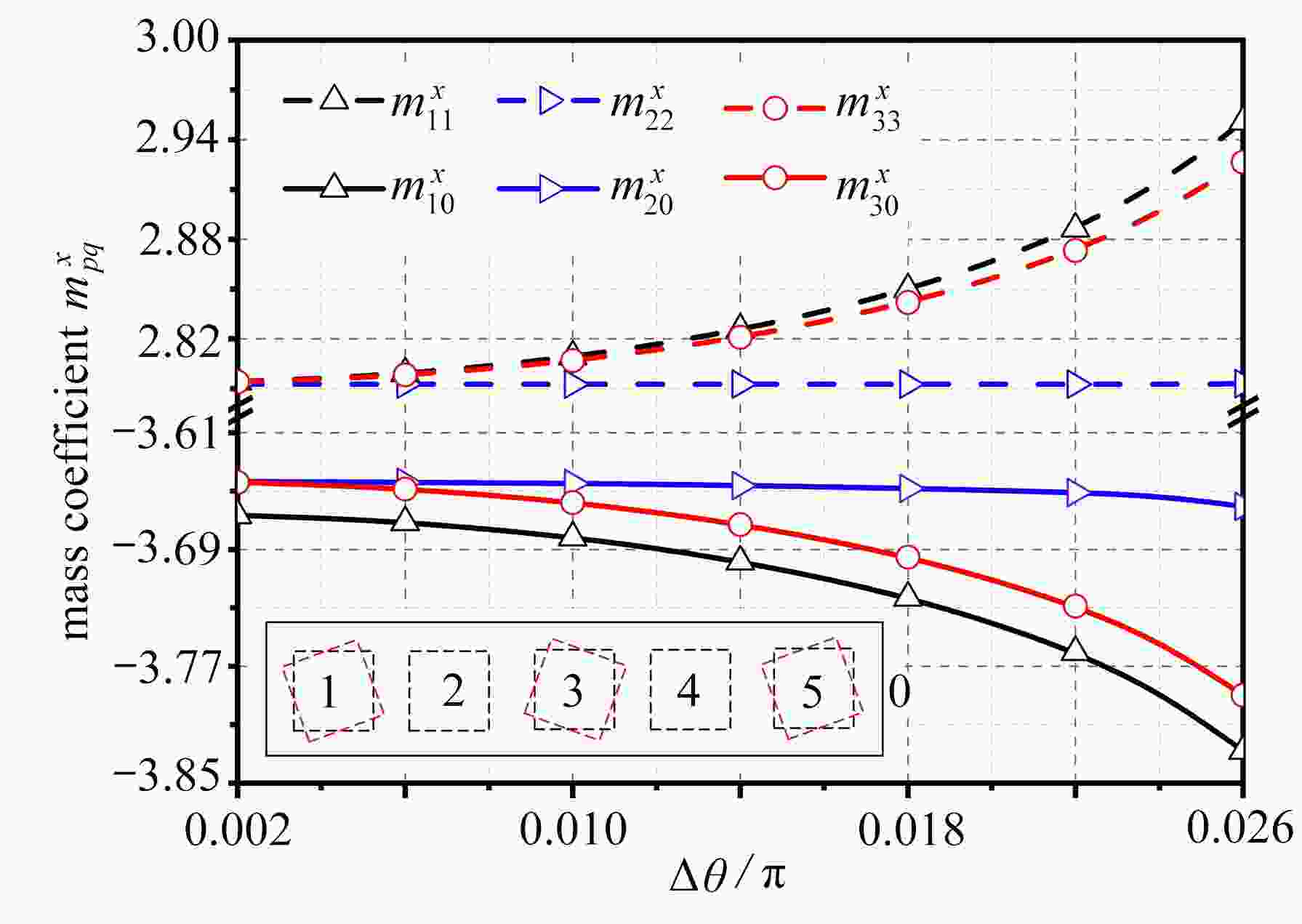
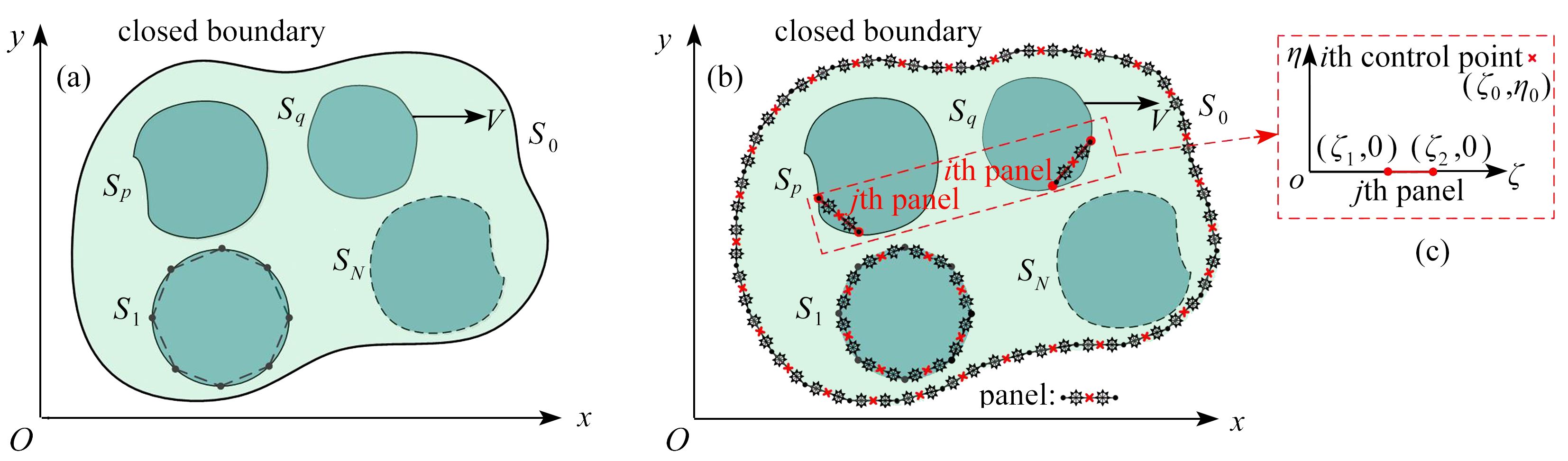
基于面元法发展了适用于计算具有任意复杂外形的刚性截面族附加流体质量系数的数值方法，并将其应用到压水堆燃料组件的计算中，分析了1 × 5组件抗震试验中由组件位置偏差所引起的附加质量系数变化规律。结果表明：该方法能解决具有复杂连续边界的刚性截面族附加质量系数计算问题；相较于组件间间隙，围板与组件间隙对质量系数的影响占主导；无论存在何种位置偏差，任意一组件在所有组件和围板上产生的沿假设运动方向与垂直假设运动方向上的附加质量系数之和分别近似为−1和0。
Abstract:A numerical method based on the panel method was developed to calculate the added fluid mass coefficients of the rigid section group with arbitrarily complex shapes, and was successfully applied to the PWR fuel assemblies. The variation law of added mass coefficients with position deviations was analyzed in the seismic test of 1×5 fuel assemblies. The results show that, this method is suitable for the calculation of the added mass coefficients of rigid section groups with complex continuous boundaries. Compared with the gap between assemblies, the gap between baffles and assemblies has a dominant influence on the added mass coefficient. Regardless of the position deviation, the sum of the added mass coefficients of all assemblies and baffles in the assumed motion direction is approximately equal to –1, and that in the perpendicular direction is approximately equal to 0.
-
Key words:
- rigid section group /
- added mass /
- panel method /
- fuel assemblies /
- position deviation
-
图 1 二维模型示意图：(a)容器截面图； (b)面元法离散图；(c)相对坐标图
注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同。
Figure 1. Schematic diagram of the 2D model: (a) the sectional view of the container; (b) the discrete graph of the panel element method; (c) the relative coordinate graph
图 2 封闭圆形容器内的一组圆形截面
Figure 2. A group of circular sections inside a closed circular container
图 5 单根燃料组件示意图：(a)单根燃料组件模型；(b) ANSYS流场网格
Figure 5. Schematic diagram of a single fuel assembly: (a) the single fuel assembly model; (b) the ANSYS flow field mesh
图 6 本文结果与ANSYS结果对比图
Figure 6. The comparison between the results of this method and the ANSYS results
表 1 截面质量系数之和
Table 1. Sums of mass coefficients of sections
p $\displaystyle \sum\limits_q {m_{pq}^x }$ $\displaystyle \sum\limits_q {m_{pq}^y }$ 3 4 6 3 4 6 ref. [6] −0.9998 −0.9997 −0.9997 −0.0001 0 0 present −1.0001 −1.0001 −1.0001 0 0 0 
下载: 导出CSV
-
[1] 张娟花. 先进核反应堆板状燃料组件流固耦合数值模拟软件的开发[D]. 硕士学位论文. 北京: 华北电力大学, 2008.ZHANG Juanhua. Development of fluid structure coupling numerical simulation software for advanced nuclear reactor plate fuel assembly[D]. Master Thesis. Beijing: North China Electric Power University, 2008. (in Chinese) [2] 岳欠杯, 刘巨保, 罗敏, 等. 圆筒流体域内管束振动与碰撞接触的流固耦合动力学方法研究[J]. 应用数学和力学, 2018, 39(5): 568-583YUE Qianbei, LIU Jubao, LUO Min, et al. A method of fluid-solid coupling dynamics for tube bundle vibration and collision in a cylinder fluid domain[J]. Applied Mathematics and Mechanics, 2018, 39(5): 568-583.(in Chinese) [3] RICCIARDI G, BELLIZZI S, COLLARD B, et al. Row of fuel assemblies analysis under seismic loading: modelling and experimental validation[J]. Nuclear Engineering and Design, 2009, 239(12): 2692-2704. doi: 10.1016/j.nucengdes.2009.08.029 [4] MAZUR V Y. Motion of a circular cylinder near a vertical wall[J]. Fluid Dynamics, 1966, 1(3): 49-51. doi: 10.1007/BF01106871 [5] MAZUR V Y. Motion of two circular cylinders in an ideal fluid[J]. Fluid Dynamics, 1970, 5(6): 969-972. [6] CHUNG H, CHEN S S. Vibration of a group of circular cylinders in a confined fluid[J]. Journal of Applied Mechanics, 1977, 44(2): 213-217. doi: 10.1115/1.3424026 [7] LAGRANGE R, DELAUNE X, PITEAU P, et al. A new analytical approach for modeling the added mass and hydrodynamic interaction of two cylinders subjected to large motions in a potential stagnant fluid[J]. Journal of Fluids and Structures, 2018, 77: 102-114. doi: 10.1016/j.jfluidstructs.2017.12.002 [8] RIGAUDEAU J, BROCHARD D, BENJEDIDIA A. Fluid structure interaction in the response of PWR fuel assemblies to horizontal seismic loads[C]//SMiRT 12 Conference. Stuttgart, Germany, 1993. [9] PAIDOUSSIS M P, SUSS S, PUSTEJOVSKY M. Free vibration of clusters of cylinders in liquid-filled channels[J]. Journal of Sound and Vibration, 1977, 55(3): 443-459. doi: 10.1016/S0022-460X(77)80025-4 [10] 赵燮霖, 冯志鹏, 蔡逢春, 等. CFD-半解析模型混合的管束结构流弹失稳预测方法[J]. 应用数学和力学, 2021, 42(3): 248-255ZHAO Xielin, FENG Zhipeng, CAI Fengchun, et al. A hybrid CFD and semi-analytical approach to predict cross-flow-induced fluidelastic instability of tube arrays[J]. Applied Mathematics and Mechanics, 2021, 42(3): 248-255.(in Chinese) [11] LI W, LU D, LIU Y. Numerical investigation on the fluid added mass of spent fuel storage rack[J]. Nuclear Engineering and Design, 2018, 339: 83-91. doi: 10.1016/j.nucengdes.2018.08.025 [12] TENG X, LIU J H, WANG H K, et al. Added mass coefficient of elastic rods in cylindrical fluid[J]. Nuclear Engineering and Design, 2019, 342: 249-256. doi: 10.1016/j.nucengdes.2018.12.010 [13] ANDERSON J. Fundamentals of Aerodynamic[M]. 5th ed. New York: McGraw-Hill Education, 2010: 282-285. [14] KATZ J, PLOTKIN A. Low-Speed Aerodynamics[M]. 2nd ed. Cambridge: Cambridge University Press, 2001: 233-235. [15] 张鸣远. 流体力学[M]. 北京: 高等教育出版社, 2010: 107-128.ZHANG Mingyuan. Fluid Mechanics[M]. Beijing: Higher Education Press, 2010: 107-128. (in Chinese) [16] 刘建, 张毅雄, 冯志鹏, 等. 正三角形排列管束结构流弹失稳流体力模型数值研究[J]. 应用数学和力学, 2020, 41(5): 499-508LIU Jian, ZHANG Yixiong, FENG Zhipeng, et al. Numerical study of fluid elastic instability fluid force model for normal-triangle tube arrays[J]. Applied Mathematics and Mechanics, 2020, 41(5): 499-508.(in Chinese) [17] ZHANG D C, LI P, WANG Q J, et al. A note on added mass of a group of sections in confined fluid: a general conclusion[J]. Archive of Applied Mechanics, 2021, 91(11): 4433-4439. doi: 10.1007/s00419-021-02050-9 -
计量
- 文章访问数: 622
- HTML全文浏览量: 262
- PDF下载量: 60
- 被引次数: 0
渝公网安备50010802005915号