面内压缩荷载作用下双层微板系统的同步/异步屈曲

张立民; 张波; 张旭; 段宇杭; 沈火明

doi:10.21656/1000-0887.430306

面内压缩荷载作用下双层微板系统的同步/异步屈曲

doi: 10.21656/1000-0887.430306

应用力学与结构安全四川省重点实验室；西南交通大学力学与航空航天学院，成都 611756

基金项目: 国家自然科学基金(11602204；11872321)；四川省自然科学基金(23NSFSC0849)

详细信息

作者简介:
张立民（1998—），男，硕士（E-mail：793220019@qq.com）

张波（1984—），男，副教授，博士，硕士生导师（通讯作者. E-mail：zhangbo2008@swjtu.edu.cn）

中图分类号: TB383；TB34；O342
计量
- 文章访问数: 545
- HTML全文浏览量: 279
- PDF下载量: 66
- 被引次数: 0
出版历程
- 收稿日期: 2022-10-05
- 修回日期: 2022-12-29
- 网络出版日期: 2023-02-02
- 刊出日期: 2023-02-15

Synchronous/Asynchronous Buckling of Double-Layered Microplate Systems

School of Mechanics and Aerospace Engineering, Southwest Jiaotong University； Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, Chengdu 611756, P.R.China

摘要

摘要:
采用修正的偶应力理论和双变量高阶剪切变形理论，发展了层间填充弹性介质的双层微板系统在面内压缩荷载作用下的屈曲模型。基于Euler-Lagrange方程推导了系统屈曲的控制微分方程，运用Navier法获得了上下层均为四边简支时系统同步/异步屈曲的解析解。通过数值算例讨论了系统各参数对其屈曲特性的影响。结果表明：系统的异步屈曲特性依赖于材料尺度参数、长宽比和弹性介质模量，而同步屈曲特性仅依赖于前两项，并且异步屈曲荷载高于同步屈曲荷载；弹性介质的Pasternak模量较之于Winkler模量对系统的屈曲特性影响更显著。
- 修正的偶应力理论 /
- 双变量高阶剪切变形理论 /
- 双层微板系统 /
- 同步/异步屈曲
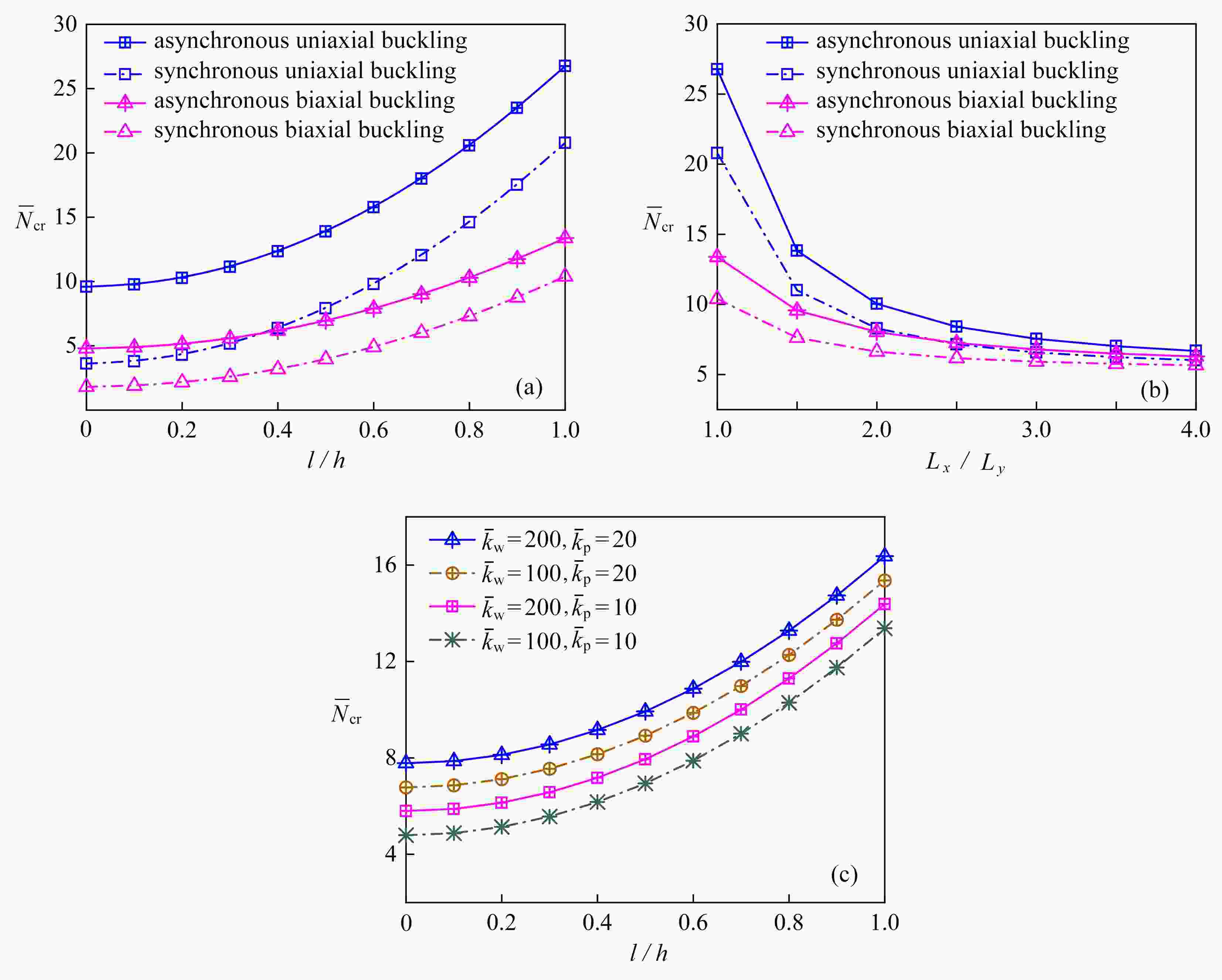
Abstract:
A linear buckling model for double-layered microplate systems filled with elastic media between layers was developed under the modified couple stress theory and the 2-variable higher-order shear deformation theory. The governing differential equations for system buckling were derived based on the Euler-Lagrange equation. With the Navier method, the synchronous and asynchronous buckling solutions were analytically obtained in the case of both upper and lower plates being simply supported on 4 edges. The influence of each parameter on the buckling characteristics of the system was discussed by numerical examples. Numerical results show that, the asynchronous buckling characteristics of the system depend on the material length scale parameter, the aspect ratio and the elastic medium modulus, while the synchronous buckling characteristics depend on the 1st 2 only; the asynchronous critical buckling load is noticeably greater than that of the synchronous buckling case; the Pasternak modulus has a more significant effect on the buckling characteristics of the system than the Winkler modulus.
- modified couple stress theory /
- 2-variable higher-order shear deformation theory /
- double-layered microplate system /
- synchronous/asynchronous buckling

HTML全文

图 1 双层微板系统示意图

Figure 1. Schematic of the double-layered microplate system

下载: 全尺寸图片幻灯片

图 2 各参数对双层微板系统临界屈曲荷载影响：(a) 无量纲材料尺度参数；(b) 长宽比；(c) 弹性介质模量

Figure 2. Effects of different parameters on the critical buckling loads on the double-layered microplate system: (a) the dimensionless material length scale parameter; (b) the aspect ratio; (c) the elastic medium modulus

下载: 全尺寸图片幻灯片

表 1 宏观单层SSSS方板的无量纲临界屈曲荷载

Table 1. Dimensionless critical buckling loads on the SSSS single-layered square macroplate

model	${{{L_x}} \mathord{\left/ {\vphantom {{{L_x}} h}} \right. } h}$
model	5	10	20	1 000
ref. [22]	3.265 3	3.786 5	3.944 3	–
ref. [23]	3.255 8	3.783 8	3.943 7	4.000
ref. [24]	3.119 0	3.729 0	3.928 0	4.000
present	3.162 0	3.744 5	3.932 3	4.000

下载: 导出CSV

表 2 尺度效应对SSSS-SSSS双层微板系统异步屈曲荷载与模态的影响

Table 2. Asynchronous buckling loads and modes of the SSSS-SSSS double-layered microplate system under uniaxial compression

下载: 导出CSV

参考文献(24)

[1]	LAM D C C, YANG F, CHONG A C M, et al. Experiments and theory in strain gradient elasticity[J]. Journal of the Mechanics and Physics of Solids, 2003, 51(8): 1477-1508. doi: 10.1016/S0022-5096(03)00053-X
[2]	LEI J, HE Y, GUO S, et al. Size-dependent vibration of nickel cantilever microbeams: experiment and gradient elasticity[J]. AIP Advances, 2016, 6(10): 105202. doi: 10.1063/1.4964660
[3]	LI Z, HE Y, ZHANG B, et al. Experimental investigation and theoretical modelling on nonlinear dynamics of cantilevered microbeams[J]. European Journal of Mechanics A: Solids, 2019, 78: 103834. doi: 10.1016/j.euromechsol.2019.103834
[4]	XIE Y, LEI J, GUO S, et al. Size-dependent vibration of multi-scale sandwich micro-beams: an experimental study and theoretical analysis[J]. Thin-Walled Structures, 2022, 175: 109115. doi: 10.1016/j.tws.2022.109115
[5]	MINDLIN R D, ESHEL N N. On first strain-gradient theories in linear elasticity[J]. International Journal of Solids and Structures, 1968, 4(1): 109-124. doi: 10.1016/0020-7683(68)90036-X
[6]	CORDERO N M, FOREST S, BUSSO E P. Second strain gradient elasticity of nano-objects[J]. Journal of the Mechanics and Physics of Solids, 2016, 97: 92-124. doi: 10.1016/j.jmps.2015.07.012
[7]	FU G, ZHOU S, QI L. On the strain gradient elasticity theory for isotropic materials[J]. International Journal of Engineering Science, 2016, 80: 28-37.
[8]	MINDLIN R D, TIERSTEN H F. Effects of couple-stresses in linear elasticity[J]. Archive for Rational Mechanics and Analysis, 1962, 11(1): 415-448. doi: 10.1007/BF00253946
[9]	YANG F, CHONG A C M, LAM D C C, et al. Couple stress based strain gradient theory for elasticity[J]. International Journal of Solids and Structures, 2002, 39(10): 2731-2743. doi: 10.1016/S0020-7683(02)00152-X
[10]	HADJESFANDIARI A R, DARGUSH G F. Couple stress theory for solids[J]. International Journal of Solids and Structures, 2011, 48(18): 2496-2510. doi: 10.1016/j.ijsolstr.2011.05.002
[11]	刘松正, 张波, 沈火明, 等. 准三维功能梯度微梁的尺度效应模型及微分求积有限元[J]. 应用数学和力学, 2021, 42(6): 623-636 LIU Songzheng, ZHANG Bo, SHEN Huoming, et al. A size-dependent quasi-3D functionally graded microbeam model and related differential quadrature finite elements[J]. Applied Mathematics and Mechanics, 2021, 42(6): 623-636.(in Chinese)
[12]	徐晓建, 邓子辰. 基于简化的应变梯度理论下Kirchhoff板模型边值问题的提法及其应用[J]. 应用数学和力学, 2022, 43(4): 363-373 XU Xiaojian, DENG Zichen. Boundary value problems of a kirchhoff type plate model based on the simplified strain gradient elasticity and the application[J]. Applied Mathematics and Mechanics, 2022, 43(4): 363-373.(in Chinese)
[13]	雷剑, 谢宇阳, 姚明格, 等. 变截面二维功能梯度微梁的振动和屈曲特性[J]. 应用数学和力学, 2022, 43(10): 1-14 LEI Jian, XIE Yuyang, YAO Mingge, et al. Vibration and buckling characteristics of two- dimensional functionally graded microbeams with variable cross-sections[J]. Applied Mathematics and Mechanics, 2022, 43(10): 1-14.(in Chinese)
[14]	MURMU T, SIENZ J, ADHIKARI S, et al. Nonlocal buckling of double-nanoplate-systems under biaxial compression[J]. Composites (Part B): Engineering, 2013, 44(1): 84-94. doi: 10.1016/j.compositesb.2012.07.053
[15]	JAMALPOOR A, AHMADI-SAVADKOOHI A, HOSSEINI M, et al. Free vibration and biaxial buckling analysis of double magneto-electro-elastic nanoplate-systems coupled by a visco- Pasternak medium via nonlocal elasticity theory[J]. European Journal of Mechanics A: Solids, 2017, 63: 84-98. doi: 10.1016/j.euromechsol.2016.12.002
[16]	SHAFIEI Z, SARRAMI-FOROUSHANI S, AZHARI F, et al. Application of modified couple-stress theory to stability and free vibration analysis of single and multi-layered graphene sheets[J]. Aerospace Science and Technology, 2020, 98: 105652. doi: 10.1016/j.ast.2019.105652
[17]	王少扬. 基于修正偶应力理论的双层粘弹性纳米板的力学特性分析[D]. 硕士学位论文. 杭州: 浙江大学, 2019. WANG Shaoyang. Mechanical characteristic analysis of double viscoelastic-nanoplates based on modified couple stress theory[D]. Master Thesis. Hangzhou: Zhejiang University, 2019. (in Chinese)
[18]	LIU J C, ZHANG Y Q, FAN L F. Nonlocal vibration and biaxial buckling of double-viscoelastic-FGM- nanoplate system with viscoelastic Pasternak medium in between[J]. Physics Letters A, 2017, 381(14): 1228-1235. doi: 10.1016/j.physleta.2017.01.056
[19]	黄明琦. 基于非局部理论的纳米板问题新解析解研究[D]. 硕士学位论文. 大连: 大连理工大学, 2020. HUANG Mingqi. New analytic solutions for nanoplates based on the nonlocal theory[D]. Master Thesis. Dalian: Dalian University of Technology, 2020. (in Chinese)
[20]	SHIMPI R P. Refined plate theory and its variants[J]. AIAA Journal, 2002, 40(1): 137-146. doi: 10.2514/2.1622
[21]	ZHANG B, LI H, LIU J, et al. Surface energy-enriched gradient elastic Kirchhoff plate model and a novel weak-form solution scheme[J]. European Journal of Mechanics A: Solids, 2021, 85: 104118. doi: 10.1016/j.euromechsol.2020.104118
[22]	THAI H T, CHOI D H. Analytical solutions of refined plate theory for bending, buckling and vibration analyses of thick plates[J]. Applied Mathematical Modelling, 2013, 37(18/19): 8310-8323.
[23]	HOSSEINI-HASHEMI S, KHORSHIDI K, AMABILI M. Exact solution for linear buckling of rectangular Mindlin plates[J]. Journal of Sound and Vibration, 2008, 315(1/2): 318-342. doi: 10.1016/j.jsv.2008.01.059
[24]	MIZUSAWA T. Buckling of rectangular mindlin plates with tapered thickness by the spline strip method[J]. International Journal of Solids and Structures, 1993, 30(12): 1663-1677. doi: 10.1016/0020-7683(93)90196-E