基于压电驱动的多材料主动结构显式拓扑优化设计

延晓晔; 赖旗; 孟尧; 张维声

doi:10.21656/1000-0887.450197

基于压电驱动的多材料主动结构显式拓扑优化设计

doi: 10.21656/1000-0887.450197

大连理工大学工程力学系，辽宁大连 116024

基金项目:

国家自然科学基金 12272075

详细信息

作者简介:
延晓晔(1997—)，男，博士生(E-mail: dllgyanxy@mail.dlut.edu.cn)

通讯作者:
张维声(1982—)，男，教授，博士，博士生导师(通讯作者. E-mail: weishengzhang@dlut.edu.cn)

中图分类号: O232
计量
- 文章访问数: 94
- HTML全文浏览量: 34
- PDF下载量: 26
- 被引次数: 0
出版历程
- 收稿日期: 2024-07-08
- 修回日期: 2024-08-04
- 刊出日期: 2024-11-01

Explicit Topology Optimization of Multi-Material Active Structures Based on Piezoelectric Actuation

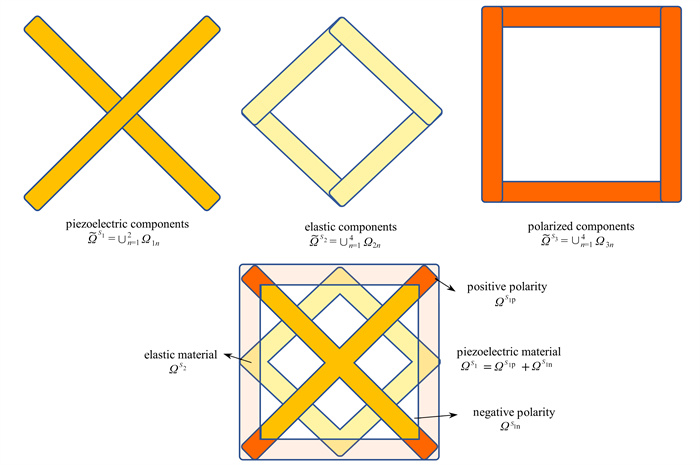
Department of Engineering Mechanics, Dalian University of Technology, Dalian, Liaoning 116024, P.R.China

摘要

摘要: 结构的轻量化设计在工业领域中一直受到高度重视. 与仅通过材料本身的刚度抵抗外界载荷作用的被动结构不同，主动结构通过主动改变结构的内力驱动变形从而实现结构轻量化. 该文提出了一种基于可移动变形组件(moving morphable components, MMC)法的压电多材料主动结构的显式拓扑优化方法. 该方法在满足位移约束的前提下，通过同时优化结构拓扑以及压电驱动器的分布实现了主动结构的总质量最小化. 为了优化极化特征以实现复杂载荷环境下的自适应压电驱动作用，引入3组独立的MMC组件分别描述弹性材料和压电材料的分布及其相应的极化特征，以得到具有显式几何描述的复合材料主动结构. 数值算例表明相比于被动结构，基于压电驱动作用的多材料主动结构能更有效地实现结构轻量化设计.
- 移动可变形组件法 /
- 拓扑优化 /
- 多材料 /
- 压电效应 /
- 主动结构
Abstract: The lightweight structure design is a crucial consideration in the industrial field. Unlike passive structures that rely solely on material stiffness to resist external loads, active structures achieve lightweighting by active change of the internal force-driven deformation. An explicit topology optimization method was introduced for piezoelectric multi-material active structures with the moving morphable components (MMC) method. The proposed method minimizes the total mass of the active structure by simultaneously optimizing the structure topology and the distribution of piezoelectric actuators while satisfying the displacement constraints. To optimize the polarization characteristics for adaptive piezoelectric actuation under complex loading conditions, 3 independent sets of MMCs were utilized. These components describe the distributions of elastic and piezoelectric materials as well as the corresponding polarization characteristics, resulting in a composite active structure with explicit geometric descriptions. Numerical examples demonstrate that, compared to passive structures, multi-material active structures based on piezoelectric actuation can realize structural lightweighting more efficiently.
- moving morphable components method /
- topology optimization /
- multi-material /
- piezoelectricity /
- active structure

HTML全文

图 1 压电多材料覆盖规则示意图

注为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.

Figure 1. An illustration of the piezoelectric multi-material overlapping scheme

下载: 全尺寸图片幻灯片

图 2 压电复合板的示意图

Figure 2. Schematic diagram of a piezoelectric composite plate

下载: 全尺寸图片幻灯片

图 3 悬臂梁模型

Figure 3. The cantilever beam model

下载: 全尺寸图片幻灯片

图 4 组件初始布局

Figure 4. The initial layout of components

下载: 全尺寸图片幻灯片

图 5 最小化质量优化结果

Figure 5. Optimized designs for weight minimization

下载: 全尺寸图片幻灯片

图 6 由外部载荷-压电驱动、外部载荷和压电驱动引起的变形图

Figure 6. Deformations caused by the external loading plus the piezoelectric actuation, the external loading and the piezoelectric actuation

下载: 全尺寸图片幻灯片

图 7 主动结构的迭代曲线

Figure 7. The convergence history of the active structure

下载: 全尺寸图片幻灯片

图 8 桥模型

Figure 8. The bridge model

下载: 全尺寸图片幻灯片

图 9 组件初始布局

Figure 9. The initial layout of components

下载: 全尺寸图片幻灯片

图 10 最小化质量优化结果

Figure 10. Optimized designs for weight minimization

下载: 全尺寸图片幻灯片

图 11 不同位移约束下的优化结果

Figure 11. Optimized designs under different displacement limits

下载: 全尺寸图片幻灯片

表 1 不同位移约束下的各材料体积分数

Table 1. The volume fractions of each material with different displacement limits

	\|u\|≤1.4 mm	\|u\|≤1.2 mm	\|u\|≤1.0 mm
V_p	0.053 2	0.073 3	0.094 7
V_m	0.266 9	0.260 2	0.264 2
V_p+V_m	0.320 1	0.333 5	0.358 9
(V_p/(V_p+V_m))/%	16.61	21.98	26.39

下载: 导出CSV

参考文献(21)

[1]	GOSSWEILER G R, BROWN C L, HEWAGE G B, et al. Mechanochemically active soft robots[J]. ACS Applied Materials & Interfaces, 2015, 7 (40): 22431-22435.
[2]	PREUMONT A. Vibration Control of Active Structures: an Introduction[M]. Array Cham: Springer, 2018.
[3]	REKSOWARDOJO A P, SENATORE G. Design of ultra-lightweight and energy-efficient civil structures through shape morphing[J]. Computers & Structures, 2023, 289 : 107149.
[4]	SOFLA A Y N, MEGUID S A, TAN K T, et al. Shape morphing of aircraft wing: status and challenges[J]. Materials & Design, 2010, 31 (3): 1284-1292.
[5]	SIGMUND O. Design of multiphysics actuators using topology optimization, part Ⅰ: one-material structures[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190 (49/50): 6577-6604.
[6]	SIGMUND O. Design of multiphysics actuators using topology optimization, part Ⅱ: two-material structures[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190 (49/50): 6605-6627.
[7]	JENSEN P D L, WANG F, DIMINO I, et al. Topology optimization of large-scale 3D morphing wing structures[J]. Actuators, 2021, 10 (9): 217. doi: 10.3390/act10090217
[8]	WANG Y, SIGMUND O. Topology optimization of multi-material active structures to reduce energy consumption and carbon footprint[J]. Structural and Multidisciplinary Optimization, 2024, 67 (1): 5. doi: 10.1007/s00158-023-03698-3
[9]	WANG Y, SIGMUND O. Multi-material topology optimization for maximizing structural stability under thermo-mechanical loading[J]. Computer Methods in Applied Mechanics and Engineering, 2023, 407 : 115938. doi: 10.1016/j.cma.2023.115938
[10]	LIND C. Two decades of negative thermal expansion research: where do we stand?[J]. Materials, 2012, 5 (6): 1125-1154. doi: 10.3390/ma5061125
[11]	黄志丹, 向楠, 苏程. 主动约束阻尼开口柱壳的NLMS反馈减振控制[J]. 应用数学和力学, 2021, 42 (7): 686-695. doi: 10.21656/1000-0887.410312 HUANG Zhidan, XIANG Nan, SU Cheng. NLMS feedback vibration control of open cylindrical shells with active constrained layer damping[J]. Applied Mathematics and Mechanics, 2021, 42 (7): 686-695. (in Chinese) doi: 10.21656/1000-0887.410312
[12]	WANG Y, LUO Z, ZHANG X, et al. Topological design of compliant smart structures with embedded movable actuators[J]. Smart Materials and Structures, 2014, 23 (4): 045024. doi: 10.1088/0964-1726/23/4/045024
[13]	ZHANG X, KANG Z. Dynamic topology optimization of piezoelectric structures with active control for reducing transient response[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 281 : 200-219. doi: 10.1016/j.cma.2014.08.011
[14]	MOLTER A, FONSECA J S O, FERNANDEZ L D S. Simultaneous topology optimization of structure and piezoelectric actuators distribution[J]. Applied Mathematical Modelling, 2016, 40 (9/10): 5576-5588.
[15]	GUO X, ZHANG W, ZHONG W. Doing topology optimization explicitly and geometrically: a new moving morphable components based framework[J]. Journal of Applied Mechanics, 2014, 81 (8): 081009. doi: 10.1115/1.4027609
[16]	ZHANG W, LAI Q, GUO X, et al. Topology optimization for the design of manufacturable piezoelectric energy harvesters using dual-moving morphable component method[J]. Journal of Mechanical Design, 2024, 146 (12): 121701. doi: 10.1115/1.4065610
[17]	HU X, LI Z, BAO R, et al. Stabilized time-series moving morphable components method for topology optimization[J]. International Journal for Numerical Methods in Engineering, 2024, 125 (20): e7562. doi: 10.1002/nme.7562
[18]	LI Z, HU X, CHEN W. Moving morphable curved components framework of topology optimization based on the concept of time series[J]. Structural and Multidisciplinary Optimization, 2023, 66 (1): 19. doi: 10.1007/s00158-022-03472-x
[19]	ZHANG W, SONG J, ZHOU J, et al. Topology optimization with multiple materials via moving morphable component (MMC) method[J]. International Journal for Numerical Methods in Engineering, 2018, 113 (11): 1653-1675. doi: 10.1002/nme.5714
[20]	HOMAYOUNI-AMLASHI A, SCHLINQUER T, MOHAND-OUSAID A, et al. 2D topology optimization MATLAB codes for piezoelectric actuators and energy harvesters[J]. Structural and Multidisciplinary Optimization, 2021, 63 (2): 983-1014. doi: 10.1007/s00158-020-02726-w
[21]	DU Z, CUI T, LIU C, et al. An efficient and easy-to-extend MATLAB code of the moving morphable component (MMC) method for three-dimensional topology optimization[J]. Structural and Multidisciplinary Optimization, 2022, 65 (5): 158. doi: 10.1007/s00158-022-03239-4